题目内容
 如图,已知四边形ABCD中,∠A=106°-α,∠ABC=74°+α,BD⊥DC于D,EF⊥DC于F,求证:∠1=∠2.
如图,已知四边形ABCD中,∠A=106°-α,∠ABC=74°+α,BD⊥DC于D,EF⊥DC于F,求证:∠1=∠2.考点:平行线的判定与性质
专题:证明题
分析:求出∠A+∠ABC=180°,根据平行线的判定定理得出AD∥BC,BD∥EF,根据平行线的性质得出∠1=∠DBC,∠2=∠DBC,即可得出答案.
解答:证明:∵∠A=106°-α,∠ABC=74°+α,
∴∠A+∠ABC=180°,
∴AD∥BC,
∴∠1=∠DBC,
∵BD⊥DC,EF⊥DC,
∴∠BDC=∠EFC=90°,
∴BD∥EF,
∴∠2=∠DBC,
∴∠1=∠2.
∴∠A+∠ABC=180°,
∴AD∥BC,
∴∠1=∠DBC,
∵BD⊥DC,EF⊥DC,
∴∠BDC=∠EFC=90°,
∴BD∥EF,
∴∠2=∠DBC,
∴∠1=∠2.
点评:本题考查了平行线的性质和判定,垂直定义的应用,能正确运用性质求出∠2=∠DBC和∠1=∠DBC是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )| A、2 | B、3 | C、4 | D、5 |
 已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC.
已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么? 在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC.
在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC. 如图,平行四边形ABCD中,点E、F分别是AD、DC边的中点,BE、BF分别与AC交于R、T.你能发现AR、RT、TC之间的关系吗?
如图,平行四边形ABCD中,点E、F分别是AD、DC边的中点,BE、BF分别与AC交于R、T.你能发现AR、RT、TC之间的关系吗?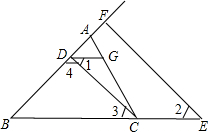 如图,
如图,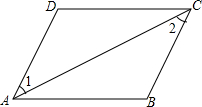 如图,∠1=∠2,∠DAB=∠BCD.给出下列结论:①AB∥DC;②AD∥BC;③∠B=∠D;④∠D=2∠DAB.其中,正确的结论有( )
如图,∠1=∠2,∠DAB=∠BCD.给出下列结论:①AB∥DC;②AD∥BC;③∠B=∠D;④∠D=2∠DAB.其中,正确的结论有( )