Question

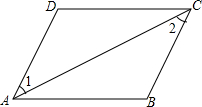如图，∠1=∠2，∠DAB=∠BCD．给出下列结论：①AB∥DC；②AD∥BC；③∠B=∠D；④∠D=2∠DAB．其中，正确的结论有（　　）

• A、1个
• B、2个
• C、3个
• D、4个

Answer 1

考点：平行线的判定与性质

专题：

分析：根据平行线的判定和已知推出AD∥BC，∠BAC=∠DCA，根据平行线的判定得出DC∥AB，证△DAC≌△BCA，推出∠D=∠B，即可得出选项．

解答：解：∵∠1=∠2，∠DAB=∠BCD，
∴AD∥BC，∠DAB-∠1=∠DCB-∠2，
∴∠BAC=∠DCA，
∴DC∥AB，
在△DAC和△BCA中

∠1=∠2 AC=AC ∠DCA=∠BAC

∴△DAC≌△BCA，
∴∠D=∠B，
根据已知不能推出∠D=2∠DAB，
即①②③正确，④错误．
故选C．

点评：本题考查了平行线的性质和判定，全等三角形的性质和判定的应用，能正确运用性质进行推理是解此题的关键，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．