题目内容
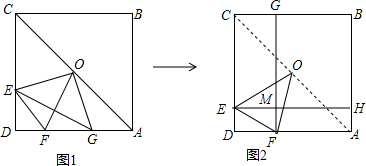
4.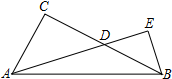 如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 过点E作EF⊥BC于F,推出△ACD∽△EDF,根据相似三角形的性质得到$\frac{DE}{AD}=\frac{EF}{AC}$,当OE⊥BC时,EF有最大值,根据勾股定理得到AB=10,由垂径定理得到BF=$\frac{1}{2}$BC=4,求得EF=2,即可得到结论.
解答 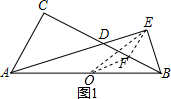 解:如图1,过点E作EF⊥BC于F,
解:如图1,过点E作EF⊥BC于F,
∵∠C=90°,
∴AC∥EF,
∴△ACD∽△EDF,
∴$\frac{DE}{AD}=\frac{EF}{AC}$,
∵AE⊥BE,
∴A,B,E,C四点共圆,
设AB的中点为O,连接OE,
当OE⊥BC时,EF有最大值,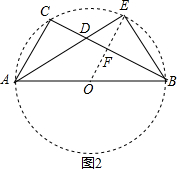
如图2,∵OE⊥BC,EF⊥BC,
∴EF,OE重合,
∵AC=6,BC=8,
∴AB=10,
∴OE=5,∵OE⊥BC,
∴BF=$\frac{1}{2}$BC=4,∴OF=3,∴EF=2,
∴$\frac{DE}{AD}=\frac{EF}{AC}$=$\frac{2}{6}$=$\frac{1}{3}$,
∴$\frac{DE}{AD}$的最大值为$\frac{1}{3}$.
点评 本题考查了相似三角形的判定和性质,四点共圆,圆周角定理,知道当OE⊥BC时,EF有最大值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.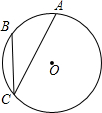 如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
 如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )| A. | π | B. | $\frac{3π}{2}$ | C. | 2π | D. | 3π |
19.2015年济南生产总值(GDP)达6280亿元,在全国排第21名,在山东排第3名.6280用科学记数法表示为( )
| A. | 62.8×102 | B. | 6.28×103 | C. | 0.628×104 | D. | 6.28×102 |
9.若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{4-2x>x-2}\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a≥-2 | B. | a<-2 | C. | a≤-2 | D. | a>-2 |
13.某家纺城的羽绒被和羊毛被这两种产品的销售价如下表:
现购买这两种产品共80条,其中购买羽绒被x条,付款总额要少于2万元,请据此列出不等式.
| 品名 | 销售价(元/条) |
| 羽绒被 | 415 |
| 羊毛被 | 150 |