题目内容
2．在样本容量为200的频数直方图中，共有3个小长方形，若第一个长方形对应的频率为10%，则第一个长方形对应的频数是20；若中间一个小长方形的高与其余两个小长方形高的和之比是2：3，则中间一组的频率为0.4．分析 根据频率=$\frac{频数}{总数}$即可求得第一个长方形对应的频数，然后根据长方形的高的比就是频率的比即可求解．
解答 解：第一个长方形对应的频数是：200×10%=20；
中间一组的频率是：$\frac{2}{2+3}$=0.4．
故答案是：20，0.4．
点评 本题考查了频率的计算公式以及频率分布直方图，理解长方形的高的比就是频率的比是关键．
练习册系列答案
天天练口算系列答案
相关题目
在平面直角坐标系xOy中，抛物线y=mx2-2mx+m+4与y轴交于点A（0，3），与x轴交于点B，C（点B在点C左侧）．
7．
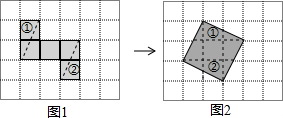如图1，每个小正方形的边长均为1，按虚线把阴影部分剪下来，用剪下来的阴影部分重新拼成如图2所示的正方形，那么所拼成的正方形的边长为（ ）
如图1，每个小正方形的边长均为1，按虚线把阴影部分剪下来，用剪下来的阴影部分重新拼成如图2所示的正方形，那么所拼成的正方形的边长为（ ）| A． | $\sqrt{5}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{6}$ |
如图所示的函数图象反映的过程是：小明从家去书店看一会儿书，又去学校取封信后马上回家，其中x表示时间（单位：小时），y表示小明离家的距离（单位：千米），则小明从学校回家的平均速度为6千米∕小时．
12．如果点A（x-y，x+y）与点B（5，-3）关于y轴对称，那么x，y的值是（ ）
| A． | x=4，y=-1 | B． | x=-4，y=-1 | C． | x=4，y=1 | D． | x=-4，y=1 |