题目内容
已知△ABC,求作一点P,使点P到∠A两边的距离相等,且PB=PC,下列确定点P的方法,正确的是( )
| A、P为∠A,∠B两角平分线的交点 |
| B、P为AC,AB两边的垂直平分线的交点 |
| C、P为AC,AB两边上的高的交点 |
| D、P为∠A的平分线与边BC的垂直平分线的交点 |
考点:角平分线的性质,线段垂直平分线的性质
专题:
分析:根据题意画出图形,由角平分线及线段垂直平分线的性质即可得出结论.
解答: 解:如图所示.
解:如图所示.
∵点P到∠A两边的距离相等,
∴点P在∠BAC的平分线上.
∵PB=PC,
∴点P在线段的垂直平分线上,
∴P为∠A的平分线与边BC的垂直平分线的交点.
故选D.
 解:如图所示.
解:如图所示.∵点P到∠A两边的距离相等,
∴点P在∠BAC的平分线上.
∵PB=PC,
∴点P在线段的垂直平分线上,
∴P为∠A的平分线与边BC的垂直平分线的交点.
故选D.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,若⊙O是以原点为圆心,2为半径的圆,则点M(1,1)在( )
| A、⊙O内 | B、⊙O外 |
| C、⊙O上 | D、不能确定 |
已知两点A(-3,y1),B(5,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y0≥y1>y2,则x0的取值范围是( )
| A、x0<5 |
| B、1<x0<5 |
| C、-3≤x0<1 |
| D、x0<1 |
 如图,经过折叠后可以围成一个正方体,折好以后与“美”字相对的字是
如图,经过折叠后可以围成一个正方体,折好以后与“美”字相对的字是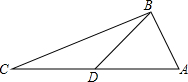 如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=
如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=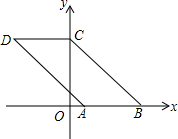 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )