题目内容
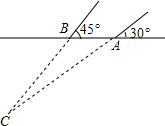 如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?
如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?考点:解直角三角形的应用
专题:
分析:过C点作AB的垂线交直线AB于点D,构建等腰Rt△BCD,在Rt△DAC中利用锐角三角函数的定义即可求出AC=2CD.然后在Rt△DAC中利用勾股定理来求CD的长度.
解答: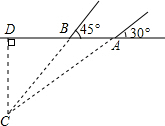 解:如图,作CD⊥AB于点D.
解:如图,作CD⊥AB于点D.
∴∠ADC=90°.
∵探测线与地面的夹角分别是30°和45°,
∴∠DBC=45°,∠DAC=30°.
∵在Rt△DBC中,∠DCB=45°,
∴DB=DC.
∵在Rt△DAC中,∠DAC=30°,
∴AC=2CD.
∵在Rt△DAC中,∠ADC=90°,AB=8,
∴由勾股定理,得 AD2+CD2=AC2.
∴(8+CD)2+CD2=(2CD)2.
∴CD=4±4
.
∵CD=4-4
不合题意,舍去.
∴CD=4+4
.
∴有金属回声的点C的深度是(4+4
)米.
 解:如图,作CD⊥AB于点D.
解:如图,作CD⊥AB于点D.∴∠ADC=90°.
∵探测线与地面的夹角分别是30°和45°,
∴∠DBC=45°,∠DAC=30°.
∵在Rt△DBC中,∠DCB=45°,
∴DB=DC.
∵在Rt△DAC中,∠DAC=30°,
∴AC=2CD.
∵在Rt△DAC中,∠ADC=90°,AB=8,
∴由勾股定理,得 AD2+CD2=AC2.
∴(8+CD)2+CD2=(2CD)2.
∴CD=4±4
| 3 |
∵CD=4-4
| 3 |
∴CD=4+4
| 3 |
∴有金属回声的点C的深度是(4+4
| 3 |
点评:本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在
、
、
、
、0.01010101…中,无理数的个数是( )
| 1 |
| π |
| 169 |
| 131 |
| 11 |
| 3 | 27 |
| A、1 | B、2 | C、3 | D、4 |
已知两点A(-3,y1),B(5,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y0≥y1>y2,则x0的取值范围是( )
| A、x0<5 |
| B、1<x0<5 |
| C、-3≤x0<1 |
| D、x0<1 |
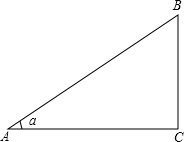 如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )
如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )| A、10tana(米) | ||||||
B、
| ||||||
| C、10sina(米) | ||||||
D、
|
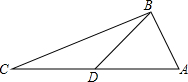 如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=
如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=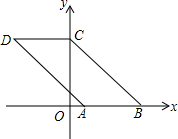 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )