题目内容
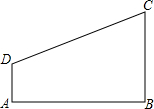 已知,如图,四边形ABCD,∠A=∠B=Rt∠
已知,如图,四边形ABCD,∠A=∠B=Rt∠(1)用直尺和圆规,在线段AB上找一点E,使得EC=ED,连接EC,ED(不写作法,保留作图痕迹);
(2)在(1)的图形中,若∠ADE=∠BEC,且CE=3,BC=
| 5 |
考点:作图—基本作图,线段垂直平分线的性质,勾股定理
专题:
分析:(1)利用作线段垂直平分线的方法,即可确定点E.
(2)先利用勾股定理求出BE的长,再利用RT△DAE≌RT△EBC即可求出AD的长.
(2)先利用勾股定理求出BE的长,再利用RT△DAE≌RT△EBC即可求出AD的长.
解答:解:(1)如图,

(2)∵△EBC是直角三角形,CE=3,BC=
,
∴BE=
=
=2,
在RT△DAE和RT△EBC中,
,
∴RT△DAE≌RT△EBC(AAS),
∴AD=BE=2.

(2)∵△EBC是直角三角形,CE=3,BC=
| 5 |
∴BE=
| CE2-BC2 |
| 9-5 |
在RT△DAE和RT△EBC中,
|
∴RT△DAE≌RT△EBC(AAS),
∴AD=BE=2.
点评:本题主要考查了基本作图,线段垂直平分线及勾股定理,解题的关键是熟记作线段垂直平分线的方法.

练习册系列答案
相关题目
在
、
、
、
、0.01010101…中,无理数的个数是( )
| 1 |
| π |
| 169 |
| 131 |
| 11 |
| 3 | 27 |
| A、1 | B、2 | C、3 | D、4 |
已知非零向量
、
和
,下列条件中,不能判定
∥
的是( )
| a |
| b |
| c |
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、|
|
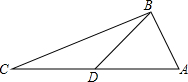 如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=
如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=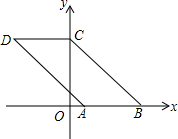 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )