题目内容
16.3•27n•81n=371,则n=10.分析 先将原式等号左边转化底数是3的幂的形式,然后根据对应相等,可以求得n的值.
解答 解:∵3•27n•81n=371
∴3×(33)n×(34)n=371,
∴3×33n×34n=371,
即37n+1=371,
∴7n+1=71,
解得n=10.
故答案为:10.
点评 本题考查幂的乘方与积的乘方、同底数幂的乘法,解题的关键是利用转化的数学思想转化为同底数幂的形式,找准对应关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.计算:$\frac{\sqrt{3}+2\sqrt{5}+\sqrt{7}}{(\sqrt{3}+\sqrt{5})(\sqrt{5}+\sqrt{7})}$=( )
| A. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | B. | $\frac{\sqrt{7}-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-\sqrt{7}}{2}$ | D. | $\frac{-\sqrt{7}-\sqrt{3}}{2}$ |
2.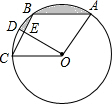 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 4π-12$\sqrt{3}$ | B. | 4π-6$\sqrt{3}$ | C. | 4π | D. | 6π |
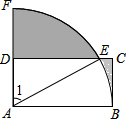 如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.
如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.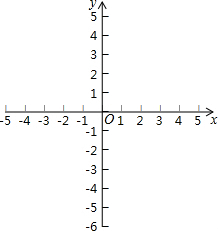 已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.
已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.