题目内容
17. 如图,A是斜边长为m的等腰直角三角形,B,C,D都是正方形.则A,B,C,D的面积的和等于$\frac{9}{4}$m2.
如图,A是斜边长为m的等腰直角三角形,B,C,D都是正方形.则A,B,C,D的面积的和等于$\frac{9}{4}$m2.
分析 根据等腰直角三角形斜边长为m,即可求得等腰直角三角形腰长,则正方形B、C、D的面积均可以求出来.
解答 解:等腰直角三角形中斜边长为m,则腰长为$\frac{\sqrt{2}}{2}$m,C,D的边长为$\frac{\sqrt{2}}{2}$m,
∴A的面积为$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$m×$\frac{\sqrt{2}}{2}$m=$\frac{1}{4}$m2,
C,D的面积为 $\frac{\sqrt{2}}{2}$m×$\frac{\sqrt{2}}{2}$m=$\frac{1}{2}$m2,
B的面积为m2,
故A、B、C、D的面积和为m2(1+$\frac{1}{2}$+$\frac{1}{2}$+$\frac{1}{4}$)=$\frac{9}{4}$m2.
故答案为:$\frac{9}{4}$m2.
点评 本题考查了勾股定理的运用,求等腰直角三角形的腰长是解本题的关键.

练习册系列答案
相关题目
12.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
根据以上信息,某同学得到以下结论:①抛物线的开口向上;②当x>-2时,y随x的增大而增大;③二次函数的最小值是-2;④抛物线的对称轴是x=-$\frac{5}{2}$,其中正确的有( )
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
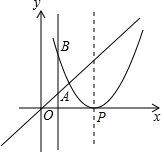 己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.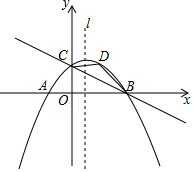 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与y轴交于点C(0,2),与x轴交于A,B两点,点A的坐标为(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与y轴交于点C(0,2),与x轴交于A,B两点,点A的坐标为(-2,0).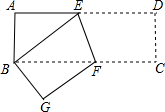 如图,在矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,求折叠后DE的长和折痕EF的长.
如图,在矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,求折叠后DE的长和折痕EF的长. 如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为∠1+∠2=90°.
如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为∠1+∠2=90°.