题目内容
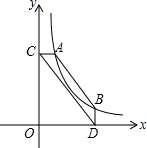 如图所示,A、B是反比例函数y=
如图所示,A、B是反比例函数y=| k |
| x |
| 1 |
| 5 |
考点:反比例函数系数k的几何意义
专题:计算题
分析:作AH⊥OD于H,如图设AC=a,则BD=a,OC=5a,所以A(a,5a),根据反比例函数图象上点的坐标特征得到B点坐标为(5a,a),再利用S矩形ACOH+S梯形ABDH-S△OCD=S四边形ABDC得到5a•a+
(a+5a)•(5a-a)-
•5a•5a=18,解得a2=4,然后根据反比例函数图象上点的坐标特征求k的值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:作AH⊥OD于H,如图,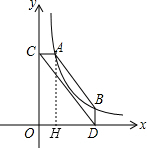
设AC=a,则BD=a,OC=5a,
∴A(a,5a),
∵A、B是反比例函数y=
上两点,而B点的纵坐标为a,
∴B点坐标为(5a,a),
∵S矩形ACOH+S梯形ABDH-S△OCD=S四边形ABDC,
∴5a•a+
(a+5a)•(5a-a)-
•5a•5a=18,解得a2=4,
∵k=a•5a=5a2,
∴k=5×4=20.
故答案为20.

设AC=a,则BD=a,OC=5a,
∴A(a,5a),
∵A、B是反比例函数y=
| k |
| x |
∴B点坐标为(5a,a),
∵S矩形ACOH+S梯形ABDH-S△OCD=S四边形ABDC,
∴5a•a+
| 1 |
| 2 |
| 1 |
| 2 |
∵k=a•5a=5a2,
∴k=5×4=20.
故答案为20.
点评:本题考查了反比例函数系数k的几何意义:在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
若
+
=
,则
+
的值为( )
| 1 |
| x |
| 1 |
| y |
| 1 |
| x+y |
| y |
| x |
| x |
| y |
| A、0 | B、1 | C、-1 | D、无法计算 |
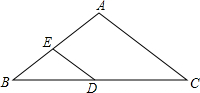 如图,在△ABC中,AB=AC,∠B=40°,D为BC上一点,DE∥AC交AB于E,则∠BED的度数为( )
如图,在△ABC中,AB=AC,∠B=40°,D为BC上一点,DE∥AC交AB于E,则∠BED的度数为( )| A、140° | B、80° |
| C、100° | D、70° |
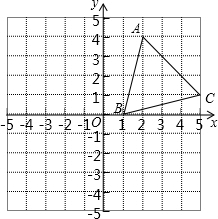 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).