题目内容
阅读并探究下列问题:
(1)如图①,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?请进行证明.
(2)如图②,将长方形纸片剪四刀,其中AB∥CD,则∠1、∠2、∠3、∠4、∠5的关系为
(3)如图③,将长方形纸片剪n刀,其中AB∥CD,则共剪出 个角.
若将剪出的角(∠A、∠C除外)分别用∠E1、∠E2、∠E3…表示,则被剪出的这些角的关系为 .
(4)如图④,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=42°,则∠GHM= .
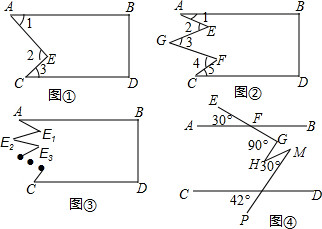
(1)如图①,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?请进行证明.
(2)如图②,将长方形纸片剪四刀,其中AB∥CD,则∠1、∠2、∠3、∠4、∠5的关系为
(3)如图③,将长方形纸片剪n刀,其中AB∥CD,则共剪出
若将剪出的角(∠A、∠C除外)分别用∠E1、∠E2、∠E3…表示,则被剪出的这些角的关系为
(4)如图④,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=42°,则∠GHM=

考点:平行线的性质
专题:
分析:(1)过E点作EF∥AB,则EF∥CD,根据两直线平行,内错角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3;
(2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5;
(3)综合(1)(2)易得开口向左的角的度数的和等于开口向右的角的度数的和.
(4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM.
(2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5;
(3)综合(1)(2)易得开口向左的角的度数的和等于开口向右的角的度数的和.
(4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM.
解答: 解:(1)∠1+∠3=∠2.
解:(1)∠1+∠3=∠2.
理由如下:过点E作EF∥AB,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠1=∠AEF,∠3=∠CEF,
∴∠1+∠3=∠AEF+∠CEF=∠AEC;
(2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,
同(1)的证明方法一样可得:∠1+∠3+∠5=∠2+∠4;
(3)规律:将长方形纸片剪n刀,其中AB∥CD,则共剪出n+1个角.
若将剪出的角(∠A、∠C除外)分别用∠E1、∠E2、∠E3…表示,则被剪出的这些角的关系为∠A+∠C+∠E2+∠E4+…+∠En-2=∠E1+∠E3+…+∠En-1.
故答案为:n+1,∠A+∠C+∠E2+∠E4+…+∠En-2=∠E1+∠E3+…+∠En-1…8分
(4)图4中,由(3)的结论得,∠BFG+∠GHM+∠MND=∠FGH+∠HMN,
∴30°+∠GHM+42°=90°+30°,
∴∠GHM=48°.
故答案为:48°.
 解:(1)∠1+∠3=∠2.
解:(1)∠1+∠3=∠2.理由如下:过点E作EF∥AB,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠1=∠AEF,∠3=∠CEF,
∴∠1+∠3=∠AEF+∠CEF=∠AEC;
(2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,
同(1)的证明方法一样可得:∠1+∠3+∠5=∠2+∠4;
(3)规律:将长方形纸片剪n刀,其中AB∥CD,则共剪出n+1个角.
若将剪出的角(∠A、∠C除外)分别用∠E1、∠E2、∠E3…表示,则被剪出的这些角的关系为∠A+∠C+∠E2+∠E4+…+∠En-2=∠E1+∠E3+…+∠En-1.
故答案为:n+1,∠A+∠C+∠E2+∠E4+…+∠En-2=∠E1+∠E3+…+∠En-1…8分
(4)图4中,由(3)的结论得,∠BFG+∠GHM+∠MND=∠FGH+∠HMN,
∴30°+∠GHM+42°=90°+30°,
∴∠GHM=48°.
故答案为:48°.
点评:此题考查了平行线的性质.此题难度适中,注意掌握辅助线的作法,注意规律:开口向左的角的度数的和等于开口向右的角的度数的和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面各组线段中,能组成三角形的是( )
| A、1,2,3 |
| B、3,4,5 |
| C、5,6,11 |
| D、6,9,16 |
数据0,3,-1,2,1的平均数和中位数分别是( )
| A、1,2 | B、1,1 |
| C、1,0 | D、2,1 |
前进乡在新农村建设中为坐落于大山中的秀水村修筑通向县成的公路投资的15万元人民币,这条5公里的路在一个月内顺利完工.15万用科学记数法表示为( )
| A、1.5×10 |
| B、1.5×105 |
| C、15×104 |
| D、1.5×104 |
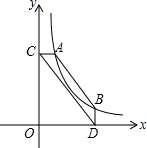 如图所示,A、B是反比例函数y=
如图所示,A、B是反比例函数y=