题目内容
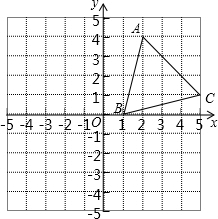 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).(1)画出△ABC关于x轴对称的△A1B1C1,其中A、B、C分别和A1、B1、C1对应,则点C1的坐标为
(2)将△ABC绕原点O逆时针旋转90°得△A2B2C2,其中A、B、C分别和A2、B2、C2对应,画出△A2B2C2,则点C2的坐标为
(3)△A1B1C1与△A2B2C2关于点
考点:作图-旋转变换
专题:
分析:(1)作出点A、B、C关于x轴对称的点,然后顺次连接即可;
(2)作出点A、B、C绕原点O逆时针旋转90°得到的点,然后顺次连接即可;
(3)根据所作图形可知,△A1B1C1与△A2B2C2关于点(
,
)对称.
(2)作出点A、B、C绕原点O逆时针旋转90°得到的点,然后顺次连接即可;
(3)根据所作图形可知,△A1B1C1与△A2B2C2关于点(
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)如图所示:△A1B1C1即为所求,其中C1点坐标为(5,-1);
(2)如图所示:△A2B2C2即为所求,其中C2点坐标为(-1,5);
(3)△A1B1C1与△A2B2C2关于点(
,
)对称.
故答案为:(5,-1);(-1,5);(
,
).

(2)如图所示:△A2B2C2即为所求,其中C2点坐标为(-1,5);
(3)△A1B1C1与△A2B2C2关于点(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(5,-1);(-1,5);(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了根据旋转对称作图,解答本题的关键是根据网格结构找出点A、B、C的对应点,然后顺次连接.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组数是勾股数的为( )
| A、32,42,52 |
| B、4,5,6 |
| C、8,15,19 |
| D、7,24,25 |
已知y=ax5+bx3+cx-5,当x=-1时,y=7,那么当x=1时,y的值是( )
| A、-17 | B、-7 | C、-12 | D、7 |
下面各组线段中,能组成三角形的是( )
| A、1,2,3 |
| B、3,4,5 |
| C、5,6,11 |
| D、6,9,16 |
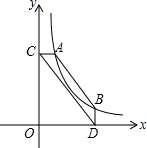 如图所示,A、B是反比例函数y=
如图所示,A、B是反比例函数y=