题目内容
16．
如图，已知∠1=∠2，AC=AD，有下列条件：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC∽△AED的条件有 （ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
分析 根据相似三角形的判定定理进行解答即可．
解答 解：∵∠1=∠2，
∴∠CAB=∠DAE；
又AC=AD；
所以要判定△ABC∽△AED，需添加的条件为：
①AB=AE，根据全等三角形的判定定理SAS可以判定△ABC≌△AED，是一种特殊的相似三角形，故正确；
③∠C=∠D（两角法），故正确；
④∠B=∠E（两角法），故正确；
故选：B．
点评 本题考查了相似三角形的判定：（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；（2）三边法：三组对应边的比相等的两个三角形相似；（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（4）两角法：有两组角对应相等的两个三角形相似．
练习册系列答案
相关题目
6．把抛物线y=-x2先向左平移1个单位，再向下平移2个单位，得到的抛物线的表达式是（ ）
| A． | y=-（x+1）2+2 | B． | y=-（x+1）2-2 | C． | y=（x+1）2-2 | D． | y=-（x-1）2+2 |
7．单项式-xn+1y3与$\frac{1}{2}$ybx2是同类项，则a，b的值分别为（ ）
| A． | a=1，b=2 | B． | a=1，b=3 | C． | a=2，b=2 | D． | a=2，b=3 |
如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=90°，AB=AC，若∠1=25°，则∠2的度数为70°．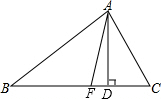
如图，AD，AF分别是△ABC的高和角平分线，已知∠B=36°，∠C=76°，则∠DAF=20°．