题目内容
14.某校准备购进50套桌椅来筹建一间多功能数学实验室,现有三种桌椅可供选择:甲种每套150元,乙种每套210元,丙种每套250元.(1)若仅选择甲、乙两种型号的桌椅,恰好用去9000元,求购买甲、乙两种型号的桌椅各多少套?
(2)若恰好用9000元同时购进甲、乙、丙三种不同型号的桌椅,请设计购买方案.
分析 (1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;
(2)根据题意可以列出相应的三元一次方程组,注意此处a、b、c均是正整数.
解答 解:(1)设购买甲种型号的桌椅x套,乙种型号的桌椅y套,
$\left\{\begin{array}{l}{x+y=50}\\{150x+210y=9000}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=25}\\{y=25}\end{array}\right.$,
答:购买甲、乙两种型号的桌椅分别是25套、25套;
(2)设购买甲种型号的桌椅a套,乙种型号的桌椅b套,丙种型号的桌椅c套,
$\left\{\begin{array}{l}{a+b+c=50}\\{150a+210b+250c=9000}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=27}\\{b=20}\\{c=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=29}\\{b=15}\\{c=6}\end{array}\right.$或$\left\{\begin{array}{l}{a=31}\\{b=10}\\{c=9}\end{array}\right.$或$\left\{\begin{array}{l}{a=33}\\{b=5}\\{c=12}\end{array}\right.$,
答:有四种设计购买方案,
方案一:购买甲种型号的桌椅27套,乙种型号的桌椅20套,丙种型号的桌椅3套,
方案二:购买甲种型号的桌椅29套,乙种型号的桌椅15套,丙种型号的桌椅6套,
方案三:购买甲种型号的桌椅31套,乙种型号的桌椅10套,丙种型号的桌椅9套,
方案四:购买甲种型号的桌椅33套,乙种型号的桌椅5套,丙种型号的桌椅12套.
点评 本题考查二元一次方程组的应用、三元一次方程组的应用,解答本题的关键是明确题意,列出相应的方程组,利用方程的思想解答.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | a<$\frac{1}{2}$ | B. | a≤$\frac{1}{2}$ | C. | a>$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
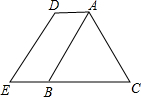 如图,在△ABC中,AB=AC,AC+BC=14,将△ABC边沿CB方向向左平移$\frac{1}{2}$BC的长,连接AD、BE、DE,求四边形ACED的周长.
如图,在△ABC中,AB=AC,AC+BC=14,将△ABC边沿CB方向向左平移$\frac{1}{2}$BC的长,连接AD、BE、DE,求四边形ACED的周长. 如图,AD是△ABC的外角平分线,且$\frac{AB}{AC}$=$\frac{\sqrt{5}+1}{2}$,求证:C是BD的黄金分割点.
如图,AD是△ABC的外角平分线,且$\frac{AB}{AC}$=$\frac{\sqrt{5}+1}{2}$,求证:C是BD的黄金分割点.