题目内容
如果将抛物线y=x2+2先向下平移1个单位,再向左平移1个单位,那么所得新抛物线的解析式是( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+1 |
| C、y=x2+1 |
| D、y=(x+1)2-1 |
考点:二次函数图象与几何变换
专题:
分析:先确定抛物线y=x2+2的顶点坐标为(0,2),根据点平移的规律得到点(0,2)平移后得到对应点的坐标为(-1,1),然后根据顶点式写出新抛物线的解析式.
解答:解:抛物线y=x2+2的顶点坐标为(0,2),把点(0,2)先向下平移1个单位,再向左平移1个单位得到对应点的坐标为(-1,1),所以所得新抛物线的解析式为y=(x+1)2+1.
故选B.
故选B.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法中正确的是( )
| A、不确定事件发生的概率是不确定的 |
| B、事件发生的概率可以等于事件不发生的概率 |
| C、事件发生的概率不可能等于0 |
| D、抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于2 |
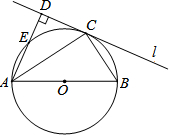 如图,AB为⊙O的直径,直线l与⊙O相切于点C,过点A作AD⊥l于点D,交⊙O于点E.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,过点A作AD⊥l于点D,交⊙O于点E. 如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.
如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.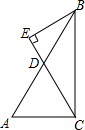 如图,△ABC中,∠ACB=90°,sinA=
如图,△ABC中,∠ACB=90°,sinA=