Question

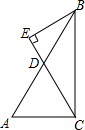如图，△ABC中，∠ACB=90°，sinA=

4

5

，BC=8，D是AB中点，过点B作直线CD的垂线，垂足为点E．
（1）求线段CD的长；
（2）求cos∠ABE的值．

Answer 1

考点：解直角三角形,勾股定理

专题：计算题

分析：（1）在△ABC中根据正弦的定义得到sinA=

BC

AB

=

4

5

，则可计算出AB=10，然后根据直角三角形斜边上的中线性质即可得到CD=

1

2

AB=5；
（2）在Rt△ABC中先利用勾股定理计算出AC=6，在根据三角形面积公式得到S_△BDC=S_△ADC，则S_△BDC=

1

2

S_△ABC，即

1

2

CD•BE=

1

2

•

1

2

AC•BC，于是可计算出BE=

24

5

，然后在Rt△BDE中利用余弦的定义求解．

解答：解：（1）在△ABC中，∵∠ACB=90°，
∴sinA=

BC

AB

=

4

5

，
而BC=8，
∴AB=10，
∵D是AB中点，
∴CD=

1

2

AB=5；
（2）在Rt△ABC中，∵AB=10，BC=8，
∴AC=

AB2-BC2

=6，
∵D是AB中点，
∴BD=5，S_△BDC=S_△ADC，
∴S_△BDC=

1

2

S_△ABC，即

1

2

CD•BE=

1

2

•

1

2

AC•BC，
∴BE=

6×8

2×5

=

24

5

，
在Rt△BDE中，cos∠DBE=

BE

BD

=

24 5

5

=

24

25

，
即cos∠ABE的值为

24

25

．

点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了直角三角形斜边上的中线性质和三角形面积公式．