题目内容
 如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.
如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.考点:相似三角形的判定
专题:证明题
分析:根据等腰三角形的性质,由AB=AC,D是BC中点得到AD⊥BC,易得∠ADC=∠BEC=90°,再加上公共角,于是根据有两组角对应相等的两个三角形相似即可得到结论.
解答:证明:∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠ADC=∠BEC,
而∠ACD=∠BCE,
∴△ACD∽△BCE.
∴AD⊥BC,
∴∠ADC=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠ADC=∠BEC,
而∠ACD=∠BCE,
∴△ACD∽△BCE.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质.

练习册系列答案
相关题目
在实数
,-
,
,
,3.14中,无理数有( )
| 22 |
| 7 |
| 5 |
| π |
| 2 |
| 3 | 8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如果将抛物线y=x2+2先向下平移1个单位,再向左平移1个单位,那么所得新抛物线的解析式是( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+1 |
| C、y=x2+1 |
| D、y=(x+1)2-1 |
若-3x2my3与2x4yn是同类项,则|m-n|的值是( )
| A、0 | B、1 | C、7 | D、-1 |
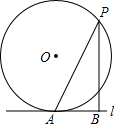 如图,直线l与半径为2的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是
如图,直线l与半径为2的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是 如图,点D是△ABC的边AC上的一点,AB2=AC•AD.
如图,点D是△ABC的边AC上的一点,AB2=AC•AD.