题目内容
阅读下列材料:
我们[a]用表示不大于a的最大整数.例如:[1.5]=1,[2]=2,[-1.5]=-2
用<b>表示不小于b的最小整数.例如:<1.5>=2,<3>=4,<-2.5>=-2
解决下列问题:
(1)[-3.5]= ,<4.5>= .
(2)若[a]=6,则a的取值范围是 ,若<b>=-1,则b的取值范围是 .
(3)已知a、b满足方程组
,求a、b的取值范围.
我们[a]用表示不大于a的最大整数.例如:[1.5]=1,[2]=2,[-1.5]=-2
用<b>表示不小于b的最小整数.例如:<1.5>=2,<3>=4,<-2.5>=-2
解决下列问题:
(1)[-3.5]=
(2)若[a]=6,则a的取值范围是
(3)已知a、b满足方程组
|
考点:取整计算
专题:
分析:(1)根据已知定义分别得出[-3.5]与<4.5>的值;
(2)利用[a]用表示不大于a的最大整数,<b>表示不大于b的最小整数,进而得出a,b的取值范围;
(3)首先解方程组,进而得出a、b的取值范围.
(2)利用[a]用表示不大于a的最大整数,<b>表示不大于b的最小整数,进而得出a,b的取值范围;
(3)首先解方程组,进而得出a、b的取值范围.
解答:解:(1)∵[a]用表示不大于a的最大整数,
∴[-3.5]=-4,
∵<b>表示不小于b的最小整数,
∴<4.5>=4.
故答案为:-4,4;
(2)∵[a]=6,
∴a的取值范围是:6≤a<7,
∵<b>=-1,
∴b的取值范围是:-1≤b<-2,
故答案为:6≤a<7;-1≤b<-2;
(3)依题意有
,
解得:
,
故2<a≤3,-2<b≤-1.
∴[-3.5]=-4,
∵<b>表示不小于b的最小整数,
∴<4.5>=4.
故答案为:-4,4;
(2)∵[a]=6,
∴a的取值范围是:6≤a<7,
∵<b>=-1,
∴b的取值范围是:-1≤b<-2,
故答案为:6≤a<7;-1≤b<-2;
(3)依题意有
|
解得:
|
故2<a≤3,-2<b≤-1.
点评:此题主要考查了取整计算,正确根据新定义得出各数的意义是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
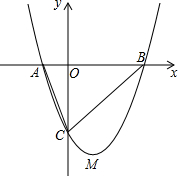 (1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;
(1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;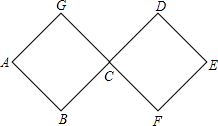 如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.当微型机器人移动了2015cm时,它停在
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.当微型机器人移动了2015cm时,它停在