题目内容
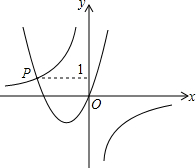如图，函数y=-| 3 |
| x |
| 3 |
| x |
考点：二次函数与不等式（组）
专题：
分析：将交点P的纵坐标代入反比例函数解析式求出横坐标，再根据函数图象写出二次函数图象在反比例函数图象下方部分的x的取值范围即可．
解答：解：∵点P的纵坐标为1，
∴-
=1，
解得x=-3，
∴点P的横坐标为-3，
∵不等式ax2+bx+
＜0可化为不等式ax2+bx＜-
，
∴不等式的解集为-3＜x＜0．
故答案为：-3＜x＜0．
∴-
| 3 |
| x |
解得x=-3，
∴点P的横坐标为-3，
∵不等式ax2+bx+
| 3 |
| x |
| 3 |
| x |
∴不等式的解集为-3＜x＜0．
故答案为：-3＜x＜0．
点评：本题考查了二次函数与不等式，利用反比例函数解析式求出交点的横坐标是解题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在△ABC中，∠C=90°，AC=15，BC=8，则点C到直线AB的距离是（ ）
A、
| ||
B、
| ||
| C、8 | ||
| D、15 |
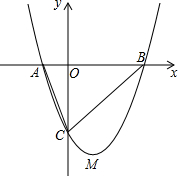（1）数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c，系数a、b、c一旦确定，抛物线的形状、大小、位置就不会变化，所以称数a、b、c为抛物线y=ax2+bx+c的特征数，记作{a，b，c}；请求出与y轴交于点C（0，-3）的抛物线y=x2-2x+k在单同学眼中的特征数；