题目内容
已知如图,△ABC中,以AB为直径作⊙O,交BC于D,交AC于E.过D点作⊙O的切线FG交AC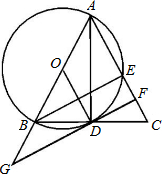 于F,交AB的延长线于G,连接AD.若AB:BG=3:1,FG⊥AC.
于F,交AB的延长线于G,连接AD.若AB:BG=3:1,FG⊥AC.
(1)求证:AD平分∠CAB;
(2)若GD=4,求BD;
(3)求AE:EF:FC.
 于F,交AB的延长线于G,连接AD.若AB:BG=3:1,FG⊥AC.
于F,交AB的延长线于G,连接AD.若AB:BG=3:1,FG⊥AC.(1)求证:AD平分∠CAB;
(2)若GD=4,求BD;
(3)求AE:EF:FC.
考点:切线的性质,全等三角形的判定与性质,勾股定理,三角形中位线定理,圆周角定理
专题:几何综合题
分析:(1)因为GF是⊙O的切线,D为切点,得到OD⊥GF,可以得到∠ODA=∠DAC,又∠ODA=∠OAD而证明AD平分∠CAB.
(2)由切割线定理可以求出AB,BG,再利用三角形相似可以求出BD:AD的比值,最后利用勾股定理在Rt△ABD中求出BD的长.
(3)证明了AD平分∠BAC,而AD⊥BC,可以证明BD=CD,又GF⊥AC得GF∥BE,得F为EC的中点,从而求出AE:EF:FC的值.
(2)由切割线定理可以求出AB,BG,再利用三角形相似可以求出BD:AD的比值,最后利用勾股定理在Rt△ABD中求出BD的长.
(3)证明了AD平分∠BAC,而AD⊥BC,可以证明BD=CD,又GF⊥AC得GF∥BE,得F为EC的中点,从而求出AE:EF:FC的值.
解答:(1)证明:∵GF是切线,
∴OD⊥GF
∴∠ODF=90°即∠ODA+∠ADF=90°
∵GF⊥AC
∴∠AFG=90°即∠ADF+∠DAC=90°
∴∠ODA=∠DAC
∵∠ODA=∠OAD
∴∠DAC=∠ODA
∴AD平分∠CAB;
(2)解:∵GD是⊙O的切线,由切割线定理得:
GD2=GB•GA
∵AB:BG=3:1,设AB=3x,则BG=x,
∴AG=4x
∴42=4x•x
解得:x=2
∴GB=2,AB=6
∵△GBD∽△GDA
∴
=
=
=
设BD=y,AD=2y,在Rt△ABD中由勾股定理得:
y2+(2y)2=62
解得:y=
,即DB=
.
(3)解:∵BE∥GF
∴
=
=
,设AE=6K,EF=2K
∵AD平分∠CAB,AD⊥BC,可以证明△ABD≌△ACD
∴BD=CD,∵BE∥GF
∴EF=FC
∴FC=2K
∴AE:EF:FC=6K:2K:2K
∴AE:EF:FC=3:1:1.
∴OD⊥GF
∴∠ODF=90°即∠ODA+∠ADF=90°
∵GF⊥AC
∴∠AFG=90°即∠ADF+∠DAC=90°
∴∠ODA=∠DAC
∵∠ODA=∠OAD
∴∠DAC=∠ODA
∴AD平分∠CAB;
(2)解:∵GD是⊙O的切线,由切割线定理得:
GD2=GB•GA
∵AB:BG=3:1,设AB=3x,则BG=x,
∴AG=4x
∴42=4x•x
解得:x=2
∴GB=2,AB=6
∵△GBD∽△GDA
∴
| BD |
| AD |
| GB |
| GD |
| 2 |
| 4 |
| 1 |
| 2 |
设BD=y,AD=2y,在Rt△ABD中由勾股定理得:
y2+(2y)2=62
解得:y=
6
| ||
| 5 |
6
| ||
| 5 |
(3)解:∵BE∥GF
∴
| AE |
| EF |
| AB |
| BG |
| 6 |
| 2 |
∵AD平分∠CAB,AD⊥BC,可以证明△ABD≌△ACD
∴BD=CD,∵BE∥GF
∴EF=FC
∴FC=2K
∴AE:EF:FC=6K:2K:2K
∴AE:EF:FC=3:1:1.
点评:本题考查了切线的性质,全等三角形的判定与性质,勾股定理,三角形的中位线定理,圆周角定理,平行线等分线段定理等知识点.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b•c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b•c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
| A、1位数 | B、2位数 |
| C、3位数 | D、4位数 |
下列哪个不是方程
+
=0的解( )
| x-y | 9 |
| 3 | x+y |
| A、(-3,-6) |
| B、(-12.5,-14.5) |
| C、(-364,-365) |
| D、(-0.5,-0.5) |
化简:
=( )
| -7-(-6)(8-9) |
| -4-(-5)(3-2) |
| A、-13 | ||
B、
| ||
| C、-1 | ||
D、
|