题目内容
2. 如图.为测量某建筑的高度.在离该建筑底部20.0米处.目测其顶部A点.视线与水平线的夹角为60°.目高1.6米.试利用相似三角形的知识.求出该建筑的高度.(精确到0.1米)
如图.为测量某建筑的高度.在离该建筑底部20.0米处.目测其顶部A点.视线与水平线的夹角为60°.目高1.6米.试利用相似三角形的知识.求出该建筑的高度.(精确到0.1米)
分析 先画出几何图形,BD=20.0m,∠ACE=60°,CD=1.6m,CE⊥AB,得到BE=CD=1.6m,CE=BD=20.0m,则在Rt△AEC中利用正切定义可得计算出AE,然后计算AE+BE即可.
解答 解:如图,BD=20.0m,∠ACE=60°,CD=1.6m,
CE⊥AB,则BE=CD=1.6m,CE=BD=20.0m,
在Rt△AEC中,∵tan∠ACE=tan60°=$\frac{AE}{CE}$,
∴AE=20.0×tan60°=20.0×$\sqrt{3}$≈34.640,
∴AB=AE+BE=34.640+1.6≈36.2(m).
答:该建筑的高度为36.2m.
点评 本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.也考查了解直角三角形.

练习册系列答案
相关题目
13.单项式-5y的系数是-5,次数是1;
单项式a3b的系数是1,次数是4;
单项式$\frac{3ab}{2}$的系数是$\frac{3}{2}$,次数是2;
单项式-5πR2的系数是-5π,次数是2.
单项式a3b的系数是1,次数是4;
单项式$\frac{3ab}{2}$的系数是$\frac{3}{2}$,次数是2;
单项式-5πR2的系数是-5π,次数是2.
14. 如图所示,∠B=90°,四边形ABCD的面积为( )
如图所示,∠B=90°,四边形ABCD的面积为( )
 如图所示,∠B=90°,四边形ABCD的面积为( )
如图所示,∠B=90°,四边形ABCD的面积为( )| A. | 36米2 | B. | 24米2 | C. | 72米2 | D. | 48米2 |
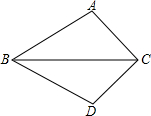 如图所示,若AB=DB,添加条件AC=DC,可用“SSS”判定△ABC≌△DBC.若用“SAS”判定,则需要添加条件∠ABC=∠DBC.
如图所示,若AB=DB,添加条件AC=DC,可用“SSS”判定△ABC≌△DBC.若用“SAS”判定,则需要添加条件∠ABC=∠DBC. 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF.
如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF.