题目内容
6. 如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).
如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).
分析 由图形列出部分点的坐标,根据坐标发现规律“A4n(-n,-n),A4n+1(n+1,-n),A4n+2(n+1,n+1),A4n+3(-n-1,n+1)”,根据该规律即可求出点A2016的坐标.
解答 解:观察,发现规律:A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),A6(2,2),A7(-2,2),A8(-2,-2),…,
∴A4n(-n,-n),A4n+1(n+1,-n),A4n+2(n+1,n+1),A4n+3(-n-1,n+1).
∵2016=4×504,
∴点A2016的坐标为(-504,-504).
故答案为:(-504,-504).
点评 本题考查了规律型中的点的坐标,解题的关键是找出规律“A4n(-n,-n),A4n+1(n+1,-n),A4n+2(n+1,n+1),A4n+3(-n-1,n+1)”.解决该题型题目时,根据图象中点的特点罗列出部分点的坐标,根据点的坐标找出规律是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
17. 如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
(1)求该抛物线的解析式
(2)连结CD,BD,求四边形OCDB的面积.
 如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)(1)求该抛物线的解析式
(2)连结CD,BD,求四边形OCDB的面积.
1.下面说法中,不正确的是( )
| A. | 绝对值最小的实数是0 | B. | 立方根最小的实数是0 | ||
| C. | 平方最小的实数是0 | D. | 算术平方根最小的实数是0 |
15.已知⊙O的半径为5cm,圆内两平行弦AB、CD的长分别为6cm、8cm,则弦AB、CD间的距离为( )
| A. | 1cm | B. | 7cm | C. | 7cm或1cm | D. | 4cm或3cm |
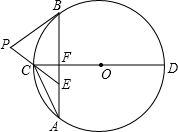 如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论:
如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论: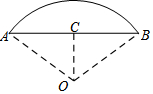 如图,弧AB的半径R为20m,AB的弦心距为OC为10m,求弓形的面积.
如图,弧AB的半径R为20m,AB的弦心距为OC为10m,求弓形的面积.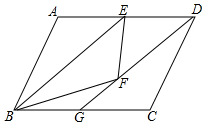 如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.
如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.