题目内容
19.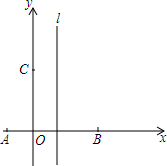 如图,在直角坐标系中,点A、B、C的坐标分别为(-1,0),(3,0),(0,3),过A、B、C三点的抛物线的对称轴为直线l,D为对称轴l上一动点.
如图,在直角坐标系中,点A、B、C的坐标分别为(-1,0),(3,0),(0,3),过A、B、C三点的抛物线的对称轴为直线l,D为对称轴l上一动点.(1)求抛物线和直线l的解析式;
(2)当AD-CD最大时求点D的坐标,并求出此时的最大值.
分析 (1)利用待定系数法即可求函数解析式;
(2)AD-CD的最大值就是线段AC的长,据此即可求解.
解答 解:(1)设抛物线的解析式是y=ax2+bx+c.
根据题意得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$
则抛物线的解析式是:y=-x2+2x+3;
抛物线的对称轴是:直线x=-$\frac{2}{2×(-1)}$=1;
(2)∵A、C的坐标分别为(-1,0)、(0,3),
∴直线AC的解析式为y=3x+3,
∵点D在直线x=1上,
∴点D的坐标为(1,6).
则AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
即AD-CD的最大值是$\sqrt{10}$.
点评 本题主要考查了待定系数法求二次函数解析式,以及轴对称的性质的应用,正确理解AD-BC最大的条件是解题的关键.

练习册系列答案
相关题目
10.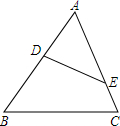 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )| A. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
11.下列哪个方程是一元二次方程( )
| A. | x+2y=1 | B. | 2x(x-1)-2x+3=0 | C. | $\frac{1}{{x}^{2}}$+4x=3 | D. | x2-2xy=0 |
9.一副扑克牌54张牌,从中任抽一张牌,抽到大王或小王的概率为( )
| A. | $\frac{1}{54}$ | B. | $\frac{1}{27}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{3}$ |
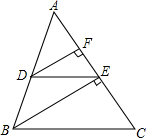 如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度.
如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度. 如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A′处,则∠A′DB度数是10°.
如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A′处,则∠A′DB度数是10°.