题目内容
18.已知|x-2|+y2+2y+1=0,则xy的值为$\frac{1}{2}$.分析 根据非负数的性质列出算式,求出x、y的值,计算即可.
解答 解:由题意得,|x-2|+(y+1)2=0,
则x-2=0,y+1=0,
解得,x=2,y=-1,
则xy=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
相关题目
9.某市举行创建文明城市志愿活动,我校初二(1)班、初二(2)班、初二(3)各班均有2名同学志愿者报名参加,现从6名同学中随机选一名志愿者,则被选中的同学恰好是初二(3)班同学的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
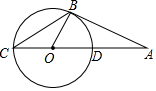 如图,AB是⊙O的切线,点C在⊙O上,且AC经过点O,若∠A=20°,AD=2,AB=4.
如图,AB是⊙O的切线,点C在⊙O上,且AC经过点O,若∠A=20°,AD=2,AB=4.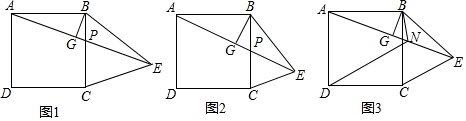
 如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.
如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.