题目内容
15.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润15元,每制造1个乙种零件可获利润26元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件,请写出此车间每天所获利润y(元)与x(名)之间的函数解析式,并写出自变量x的取值范围.分析 根据人数乘以生产效率,可得产量,根据产量乘以每件的利润,可得总利润,根据人数都是正数,可得自变量的取值范围.
解答 解:车间每天安排x名工人制造甲种零件,(20-想)人制造乙种零件,由题意,得
y=6x×15+(20-x)×5×26;
由人数都是非负数,得
x≥0,20-x≥0,
解得0≤x≤20,
自变量x的取值范围是0≤x≤20.
点评 本题考查了函数关系式,利用产量乘以每件的利润得出总利润是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8.下列各式中,可分解因式的只有( )
| A. | x2+y2 | B. | x2-y3 | C. | ma+nb | D. | -x2+y2 |

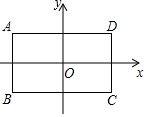 如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若A点的坐标为(-4,3).
如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若A点的坐标为(-4,3). 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.