题目内容
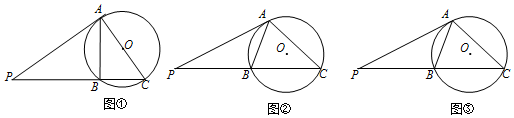
15.初步探究如图①,过点P的两条直线分别与⊙O相切于点A,与⊙O相交于B、C两点,且AC恰好经过圆心O.求证△PAB∽△PCA.
进一步探究
如图②若其他条件不变,但AC不经过圆心O.上述结论是否成立?请说明理由.
尝试应用
如图③,PA=3,PB=$\sqrt{3}$,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.
分析 (1)由PA与⊙O相切,得到∠PAC=90°.根据余角的想知道的∠PAB=∠C.于是得到结论;
(2)连接AO,延长AO交⊙O于D,连接BD.根据切线的性质得到∠PAD=90°.根据余角的性质得到∠PAB=∠D.于是得到结论;
(3)过O作OD⊥BC于D,连接OB,则OB=2,OD为直线PC上一点D与圆心O的最短距离,根据切割线定理得到PC=3$\sqrt{3}$,根据勾股定理即可得到结论.
解答 解:(1)∵PA与⊙O相切,
∴∠PAC=90°.
∴∠BAD+∠PAB=90°.
∵AC是⊙O的直径,
∴∠BAD+∠C=90°.
∴∠PAB=∠C.
又∵∠P=∠P,
∴△PAB∽△PCA;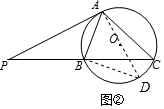
(2)成立.连接AO,延长AO交⊙O于D,连接BD.
∵PA与⊙O相切,
∴∠PAD=90°.
∴∠BAD+∠PAB=90°.
∵AD是⊙O的直径,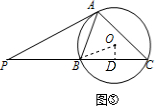
∴∠BAD+∠D=90°.
∴∠PAB=∠D.
又∵∠C=∠D,
∴∠PAB=∠C.
又∵∠P=∠P,
∴△PAB∽△PCA;
(3)过O作OD⊥BC于D,连接OB,
则OB=2,OD为直线PC上一点D与圆心O的最短距离,
∵PA是⊙O的切线,
∴PA2=PB•PC,
∴PC=3$\sqrt{3}$,
∴BC=2$\sqrt{3}$,
∵BD⊥BC,
∴BD=$\sqrt{3}$,
∴OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=1.
点评 本题考查了切线的性质,相似三角形的判定,圆周角定理,切割线定理,正确的作出辅助线是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
5.若a与-5互为相反数,则a的值是( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
6.用配方法解一元二次方程x2-4x=5时,下列配方正确的是( )
| A. | (x-2)2=9 | B. | (x-2)2=1 | C. | (x+2)2=9 | D. | (x+2)2=1 |
3.-$\frac{1}{3}$的倒数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
8.下列二次根式,化简结果为-4( )
| A. | $\sqrt{(-4)^{2}}$ | B. | (-$\sqrt{4}$)2 | C. | -$\sqrt{{4}^{2}}$ | D. | $\sqrt{{4}^{2}}$ |
 如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB、BC分别交于点D、E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.
如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB、BC分别交于点D、E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.