题目内容
如图(1)是长方形纸条,将纸条沿EF折叠成图(2),再沿AF折叠成图(3),已知图(3)中的∠CFE=120°,则图(1)中∠DEF的度数是 .


考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:先根据∠CFE=120°求出∠GEF的度数,在图(2)中求出∠CFG的度数,再根据DG∥CF得出∠DGF的数,由三角形外角的性质得出∠GEF的度数,由图形翻折变换的性质即可得出结论.
解答:解:∵图(3)中的∠CFE=120°,
∴∠GFE=
=30°.
∴图(2)中,∠CFG=120°+30°=150°,∠EFG=
=15°,
∵DG∥CF,
∴∠DGF=180°-150°=30°.
∵∠DGF是△GEF的外角,
∴∠GEF=∠DGF-∠EFG=30°-15°=15°.
∴图(1)中,∠DEF=2∠GEF=30°.
故答案为:30°.
∴∠GFE=
| 180°-120° |
| 2 |
∴图(2)中,∠CFG=120°+30°=150°,∠EFG=
| 180°-150° |
| 2 |
∵DG∥CF,
∴∠DGF=180°-150°=30°.
∵∠DGF是△GEF的外角,
∴∠GEF=∠DGF-∠EFG=30°-15°=15°.
∴图(1)中,∠DEF=2∠GEF=30°.
故答案为:30°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列四个图形中,是中心对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
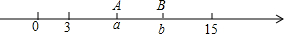 如图,一根木棒放在数轴上,木棒的左端与数轴上的数a表示的点A重合,右端与数轴b表示的点B重合,若将木棒沿数轴右方向移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为15,若将木棒沿数轴向左水平移动,则当它的右端点移动到A点时,它的左端点在数轴上所对应的数为3.
如图,一根木棒放在数轴上,木棒的左端与数轴上的数a表示的点A重合,右端与数轴b表示的点B重合,若将木棒沿数轴右方向移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为15,若将木棒沿数轴向左水平移动,则当它的右端点移动到A点时,它的左端点在数轴上所对应的数为3. 求阴影部分面积.
求阴影部分面积.