题目内容
10．
如图，在平行四边形ABCD中，对角线AC、BD相交于点O，如果AC=12，BD=8，AB=x，那么x的取值范围是（ ）| A． | 2＜x＜10 | B． | 4＜x＜20 | C． | 8＜x＜12 | D． | 4＜x＜6 |
分析 由在平行四边形ABCD中，AC=12，BD=8，根据平行四边形的对角线互相平分，即可求得OA与OB的长，然后由三角形的三边关系，求得x的取值范围．
解答 解：∵在平行四边形ABCD中，AC=12，BD=8，
∴OA=$\frac{1}{2}$AC=6，OB=$\frac{1}{2}$BD=4，
∵AB=x，
∴x的取值范围是：2＜x＜10．
故选A．
点评 此题考查了平行四边形的性质以及三角形的三边关系．注意平行四边形的对角线互相平分．
练习册系列答案
阅读快车系列答案
相关题目
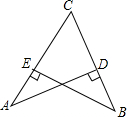如图，从小丽家C到学校A和菜市场B的夹角∠ACB是锐角，又知道从小丽家到学校A和到菜市场B的距离相等，小丽说学校A到路BC的距离AD与菜市场B到路AC的距离BE相等，你认为她说得有道理吗？请说明理由．
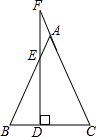如图所示，在△ABC中，AB=AC，点D是底边BC上的一个动点，过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F．
5．对于非零的两个实数a、b，规定a⊕b=$\frac{1}{b}$-$\frac{1}{a}$．若1⊕（x+1）=1，则x的值为（ ）
| A． | $\frac{3}{2}$ | B． | 1 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
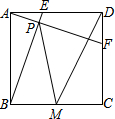如图，正方形ABCD中，AB=2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为$\sqrt{10}$．
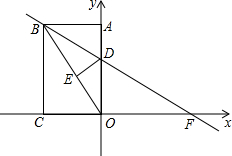如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（-12，16），矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．