题目内容
20.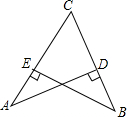 如图,从小丽家C到学校A和菜市场B的夹角∠ACB是锐角,又知道从小丽家到学校A和到菜市场B的距离相等,小丽说学校A到路BC的距离AD与菜市场B到路AC的距离BE相等,你认为她说得有道理吗?请说明理由.
如图,从小丽家C到学校A和菜市场B的夹角∠ACB是锐角,又知道从小丽家到学校A和到菜市场B的距离相等,小丽说学校A到路BC的距离AD与菜市场B到路AC的距离BE相等,你认为她说得有道理吗?请说明理由.
分析 根据AAS证明△CAD≌△CBD,由全等三角形对应边相等即可得到AD=BE.
解答 解:学校A到路BC的距离AD与菜市场B到路AC的距离BE相等.
理由如下:
在△CAD与△CBD中,
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠C=∠C}\\{AC=BC}\end{array}\right.$,
∴△CAD≌△CBD(AAS),
∴BE=AD.
点评 本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
2. 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )| A. | 60° | B. | 90° | C. | 100° | D. | 120° |
15.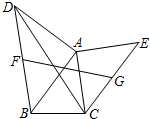 如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则$\frac{CD}{FG}$的值等于( )
如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则$\frac{CD}{FG}$的值等于( )
 如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则$\frac{CD}{FG}$的值等于( )
如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则$\frac{CD}{FG}$的值等于( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
12.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三个内角比为1:2:1 | B. | 三边之比为1:2:$\sqrt{5}$ | ||
| C. | 三边之比为$\sqrt{3}$:2:$\sqrt{5}$ | D. | 三个内角比为1:2:3 |
9.二元一次方程x+2y=5在实数范围内的解( )
| A. | 只有1个 | B. | 只有2个 | C. | 只有3个 | D. | 有无数个 |
10. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )| A. | 2<x<10 | B. | 4<x<20 | C. | 8<x<12 | D. | 4<x<6 |
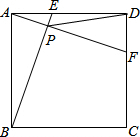 如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,则线段DP的最小值为$\sqrt{5}$-1.
如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,则线段DP的最小值为$\sqrt{5}$-1. 如图,在平面直角坐标系xOy,直线y=x+1与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
如图,在平面直角坐标系xOy,直线y=x+1与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.