题目内容
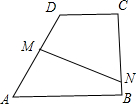如图，直角梯形ABCD中，AB∥CD，∠B=90°，AB=8，BC=10，CD=5，AD的中垂线MN交BC于N，求BN的长．考点：直角梯形
专题：
分析：连接DN，AN，根据线段垂直平分线得出DN=AN，根据勾股定理得出关于BN的方程，求出方程的解即可．
解答：解：
∵直角梯形ABCD中，AB∥CD，∠B=90°，
∴∠C=90°，
连接AN、DN，
∵AD的中垂线MN，
∴AN=DN，
由勾股定理得：DN2=DC2+CN2，AN2=AB2+BN2，
∴DC2+CN2=AB2+BN2，
∵AB=8，BC=10，CD=5，
∴82+BN2=52+（10-BN）2，
解得：BN=
．
∵直角梯形ABCD中，AB∥CD，∠B=90°，
∴∠C=90°，
连接AN、DN，
∵AD的中垂线MN，
∴AN=DN，
由勾股定理得：DN2=DC2+CN2，AN2=AB2+BN2，
∴DC2+CN2=AB2+BN2，
∵AB=8，BC=10，CD=5，
∴82+BN2=52+（10-BN）2，
解得：BN=
| 61 |
| 20 |
点评：本题考查了勾股定理，线段垂直平分线，直角梯形的应用，解此题的关键是得出关于BN的方程，题目比较好，难度适中．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
如图，已知⊙O是△ABC的外接圆，点I是△ABC的内心，延长AI交BC于点E，交⊙O于点D，连接BD、DC、BI．求证：DB=DC=DI．
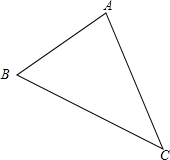已知△ABC，