题目内容
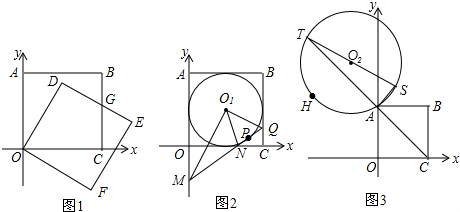
如图1,在直角坐标系中,正方形OABC的两边OC、OA分别在x轴、y轴上,A点的坐标为(O,4).
(1)则B的坐标为 ;
(2)将正方形OABC绕点O顺时针旋转30°,得正方形ODEF,边DE交BC于G,求G点坐标.
(3)如图2,⊙O1与正方形ABCO四边都相切,直线MQ切⊙O1于P,分别交y轴、x轴、线段BC于M、N、Q.求证:O1N平分∠MO1Q.
(4)延长BA至H,使AH=AB,在CA的延长线上任取一点T,经过A、H、T作⊙O2,过T作直径TS,连AS(图3),试问,T在运动过程中,AT-AS的值是否为定值?若是,定值为 ;若不是,请说明理由.
(1)则B的坐标为
(2)将正方形OABC绕点O顺时针旋转30°,得正方形ODEF,边DE交BC于G,求G点坐标.
(3)如图2,⊙O1与正方形ABCO四边都相切,直线MQ切⊙O1于P,分别交y轴、x轴、线段BC于M、N、Q.求证:O1N平分∠MO1Q.
(4)延长BA至H,使AH=AB,在CA的延长线上任取一点T,经过A、H、T作⊙O2,过T作直径TS,连AS(图3),试问,T在运动过程中,AT-AS的值是否为定值?若是,定值为

考点:圆的综合题
专题:
分析:(1)根据正方形四边相等的性质求B点到x轴,y轴的距离,即可求得B点坐标;
(2)连接OG,由题可知旋转角∠AOD、∠FOC的度数为30°,进而求出∠GOC的度数,再利用三角函数求出G点坐标;
(3)由切线长定理证得∠MO1Q=90°,由切线长定理或其他方法证得∠NO1Q=45°,O1N平分∠MO1Q;
(4)在AT上取点V,使TV=AS,构造出全等三角形△HTV≌△HSA,判断出△HAV为等腰直角三角形,求得AT-AS=AV=
为定值.
(2)连接OG,由题可知旋转角∠AOD、∠FOC的度数为30°,进而求出∠GOC的度数,再利用三角函数求出G点坐标;
(3)由切线长定理证得∠MO1Q=90°,由切线长定理或其他方法证得∠NO1Q=45°,O1N平分∠MO1Q;
(4)在AT上取点V,使TV=AS,构造出全等三角形△HTV≌△HSA,判断出△HAV为等腰直角三角形,求得AT-AS=AV=
| 2 |
解答: 解:(1)∵四边形OABC是正方形且A点的坐标为(O,4),
解:(1)∵四边形OABC是正方形且A点的坐标为(O,4),
∴AB=BC=OA=4,
∴B点的坐标为(4,4);
(2)连接OG,如图1
∵正方形OABC绕点O顺时针旋转30°得正方形ODEF,
∴∠AOD=30°,
∴∠DOC=60°,
在Rt△ODG和Rt△OCG中,
,
∴Rt△ODG≌Rt△OCG(HL),
∴∠DOG=∠COG,
∴∠COG=30°,
∵A点的坐标为(O,4),四边形OABC为正方形,
∴OC=OA=4,
∴CG=tan30°OC=
OC=
,
∴G点的坐标为(4,
);
(3)证明:∵BQ∥AM,
∴∠BQM+∠AMQ=180°,
根据切线长定理,∠O1QM+∠O1MQ=180°×
=90°,
∴∠MO1Q=180°-90°=90°,
由切线长定理∠NO1Q=45°,
∴O1N平分∠MO1Q;
(4)如图2, 在AT上取点V,使TV=AS,即AT-AS=AV,
在AT上取点V,使TV=AS,即AT-AS=AV,
∵TS是直径,
∴∠THS=∠TAS=90°,
∵AH=AB,
∴点H坐标为(-4、4),
又∵∠OAC=45°,
∴∠TAH=45°,
∵∠THS=∠TAS=90°,
∴∠TSH=45°,
∴HT=HS;
在△HTV≌△HSA,
,
∴△HTV≌△HSA(SAS),
∴△HAV为等腰直角三角形,
∴AT-AS=AV=4
.
∴AT-AS的值为定值4
.
 解:(1)∵四边形OABC是正方形且A点的坐标为(O,4),
解:(1)∵四边形OABC是正方形且A点的坐标为(O,4),∴AB=BC=OA=4,
∴B点的坐标为(4,4);
(2)连接OG,如图1
∵正方形OABC绕点O顺时针旋转30°得正方形ODEF,
∴∠AOD=30°,
∴∠DOC=60°,
在Rt△ODG和Rt△OCG中,
|
∴Rt△ODG≌Rt△OCG(HL),
∴∠DOG=∠COG,
∴∠COG=30°,
∵A点的坐标为(O,4),四边形OABC为正方形,
∴OC=OA=4,
∴CG=tan30°OC=
| ||
| 3 |
4
| ||
| 3 |
∴G点的坐标为(4,
| 4 |
| 3 |
| 3 |
(3)证明:∵BQ∥AM,
∴∠BQM+∠AMQ=180°,
根据切线长定理,∠O1QM+∠O1MQ=180°×
| 1 |
| 2 |
∴∠MO1Q=180°-90°=90°,
由切线长定理∠NO1Q=45°,
∴O1N平分∠MO1Q;
(4)如图2,
 在AT上取点V,使TV=AS,即AT-AS=AV,
在AT上取点V,使TV=AS,即AT-AS=AV,∵TS是直径,
∴∠THS=∠TAS=90°,
∵AH=AB,
∴点H坐标为(-4、4),
又∵∠OAC=45°,
∴∠TAH=45°,
∵∠THS=∠TAS=90°,
∴∠TSH=45°,
∴HT=HS;
在△HTV≌△HSA,
|
∴△HTV≌△HSA(SAS),
∴△HAV为等腰直角三角形,
∴AT-AS=AV=4
| 2 |
∴AT-AS的值为定值4
| 2 |
点评:本题考查了圆的综合题.难度在于(1)此题不仅要熟悉旋转角,还要知道旋转不变性,并联系特殊三角形用勾股定理解答;(2)运用切割线定理是解答此题的关键;(3)构造全等三角形,比作辅助线难度要大,但确是一种有效的解题方法.

练习册系列答案
相关题目
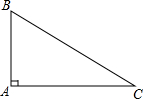 如图,在△ABC中,AB⊥AC,垂足为A.
如图,在△ABC中,AB⊥AC,垂足为A.
 如图,在正△ABC中,D、E分别是BC、AC上一点,AE=CD,AD与BE交于点F,AF=
如图,在正△ABC中,D、E分别是BC、AC上一点,AE=CD,AD与BE交于点F,AF=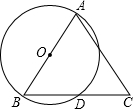 如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状:
如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: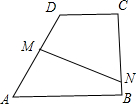 如图,直角梯形ABCD中,AB∥CD,∠B=90°,AB=8,BC=10,CD=5,AD的中垂线MN交BC于N,求BN的长.
如图,直角梯形ABCD中,AB∥CD,∠B=90°,AB=8,BC=10,CD=5,AD的中垂线MN交BC于N,求BN的长.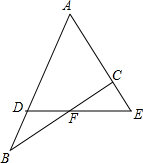 如图所示,已知AD:DB=7:2,AC:CE=4:3,则BF:FC=
如图所示,已知AD:DB=7:2,AC:CE=4:3,则BF:FC=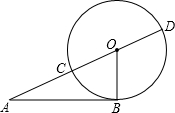 如图,在Rt△ABO中,∠B=Rt∠,以O为圆心,OB为半径画圆,分别交AO和AO的延长线于C、D,若OB=1,AB=3;
如图,在Rt△ABO中,∠B=Rt∠,以O为圆心,OB为半径画圆,分别交AO和AO的延长线于C、D,若OB=1,AB=3;