题目内容
8.计算:(1)${(\frac{1}{3})^{-1}}-|{-2+\sqrt{3}tan{{45}°}}|+{(\sqrt{2}-1.41)^0}$;
(2)$\frac{{a}^{2}}{a+1}$-a+1.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算,即可得到结果.
解答 解:(1)原式=3-2+$\sqrt{3}$+1=2+$\sqrt{3}$;
(2)原式=$\frac{{a}^{2}}{a+1}$-$\frac{(a+1)(a-1)}{a+1}$=$\frac{1}{a+1}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.若不等式组$\left\{\begin{array}{l}{x<m}\\{x≥6}\end{array}\right.$无解,则m的取值范围是( )
| A. | m≥6 | B. | m≤6 | C. | m>6 | D. | m<6 |
8.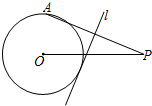 如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
 如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )| A. | 10 | B. | $\frac{21}{2}$ | C. | 11 | D. | $\frac{43}{4}$ |