题目内容
7.平行四边形的两条对角线的长分别是10和12,则边长x的取值范围是1<x<11.分析 根据平行四边形对角线互相平分求出两对角线的一半,再根据三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求解.
解答 解:∵平行四边形的两条对角线的长分别是10和12,
∴两对角线的一半分别是5,6,
∵6-5=1,6+5=11,
∴边长x的取值范围是1<x<11.
故答案为:1<x<11.
点评 本题考查了平行四边形对角线互相平分的性质,三角形的三边关系,熟记性质并考虑利用三边关系求解是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
2.$\sqrt{(4-a)(a-2)^{2}}$=(a-2)$\sqrt{4-a}$成立的条件是( )
| A. | a≤2 | B. | a≤4 | C. | 2≤a≤4 | D. | a≥2 |
12.下列变量之间的关系不是函数关系的是( )
| A. | 长方形的面积一定,其长与宽 | B. | 正方形的周长与面积 | ||
| C. | 长方形的周长与面积 | D. | 圆的面积与圆的半径 |
 如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为( )
如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为( )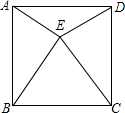 如图,正方形ABCD内的△BEC为正三角形,求∠DEA的度数.
如图,正方形ABCD内的△BEC为正三角形,求∠DEA的度数.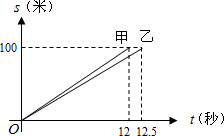 假定甲乙两人在一次赛跑中,路程S(米)与时间t(秒)的关系式如图所示,那么可以知道:
假定甲乙两人在一次赛跑中,路程S(米)与时间t(秒)的关系式如图所示,那么可以知道: