题目内容
18．
如图，在△ABC中，∠BAC=90°，AC=6，BC=10，过点A的直线DE∥BC，∠ABC与∠ACB的平分线分别交DE于E、D，则DE的长为（ ）| A． | 14 | B． | 16 | C． | 18 | D． | 20 |
分析 在Rt△ABC中，利用勾股定理求得AB=10；然后由平行线的性质、角平分线的性质推知∠E=∠ABE，则AB=AE．同理可得，AD=AC，所以线段DE的长度转化为线段AB、AC的和．
解答 解：在Rt△ABC中，∠BAC=90°，AC=6 BC=10 根据勾股定理，得AB=8，
∵DE∥BC，
∴∠E=∠EBC．
∵BE平分∠ABC，
∴∠ABE=∠EBC，
∴∠E=∠ABE，
∴AB=AE．
同理可得：AD=AC，
∴DE=AD+AE=AB+AC=14．
故选A
点评 本题综合考查了勾股定理、平行线的性质以及等腰三角形的判定与性质．注意，勾股定理应用的前提条件是在直角三角形中．
练习册系列答案
相关题目
13．
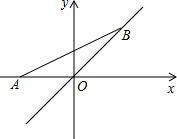如图，点A的坐标为（-1，0）点B（a，a），当线段AB最短时，点B的坐标为（ ）
如图，点A的坐标为（-1，0）点B（a，a），当线段AB最短时，点B的坐标为（ ）| A． | （0，0） | B． | （$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$） | C． | （-$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$） | D． | （-$\frac{1}{2}$，-$\frac{1}{2}$） |
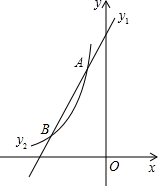如图，已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$（x＜0）的图象在第二象限内相交于A、B两点，其中点A的纵坐标为4．
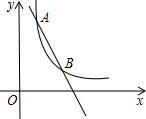如图，点A（1，6）是反比例函数y=$\frac{k}{x}$（x＞0）的图象上一个点，点B（m，n）（m＞1）是该函数图象上一动点，过A点分别作AD⊥x轴，AC⊥y轴，垂足分别为D，C，过B点分别作BF⊥x轴，BE⊥y轴，垂足分别为F，E，设AD交BE于G点，连接AB．