题目内容
 已知:如图AB∥DE,AC∥DF,BE=CF,此时AB与DE有什么关系?试说明理由.
已知:如图AB∥DE,AC∥DF,BE=CF,此时AB与DE有什么关系?试说明理由.考点:全等三角形的判定与性质
专题:
分析:根据AB∥DE,AC∥DF,可得∠ABC=∠DEF和∠ACB=∠DFE,根据BE=CF可得BC=EF,即可证明△ABC≌△DEF,根据全等三角形对应边相等的性质即可解题.
解答:解:此时AB=DE,
理由:∵AB∥DE,
∴∠ABC=∠DEF,
∵AC∥DF,
∴∠ACB=∠DFE,
∵BE=CF,
∴BE+EC=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE.
理由:∵AB∥DE,
∴∠ABC=∠DEF,
∵AC∥DF,
∴∠ACB=∠DFE,
∵BE=CF,
∴BE+EC=CF+CE,即BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(ASA),
∴AB=DE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABC≌△DEF是解题的关键.

练习册系列答案
相关题目
在3.14,
,0,
,
,0.150250015…中,无理数有( )
| 13 |
| 3 | 8 |
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm)
用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm)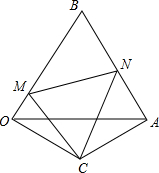 如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是
如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是
 阅读下面材料并回答问题:
阅读下面材料并回答问题: