题目内容
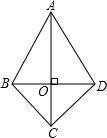 如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=
如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=| 2 |
| A、100° | B、105° |
| C、85° | D、95° |
考点:含30度角的直角三角形,等腰直角三角形
专题:
分析:先由△BCD是等腰直角三角形,得出∠CDB=∠CBD=45°,再证明△COD是等腰直角三角形,得出CD=
OD,而AD=
CD,则AD=2OD.于是在直角△AOD中,根据sin∠OAD=
=
,得出∠OAD=30°,∠ODA=60°,然后根据∠ADC=∠ODA+∠CDO即可求解.
| 2 |
| 2 |
| OD |
| AD |
| 1 |
| 2 |
解答:解:∵△BCD中,∠BCD=90°,BC=CD,
∴∠CDB=∠CBD=45°,
∵AC⊥BD于点O,
∴∠COD=90°,∠OCD=45°,△COD是等腰直角三角形,
∴CD=
OD,
∵AD=
CD,
∴AD=
CD=
×
OD=2OD.
在直角△AOD中,∠AOD=90°,
∴sin∠OAD=
=
,
∴∠OAD=30°,
∴∠ODA=90°-30°=60°,
∴∠ADC=∠ODA+∠CDO=60°+45°=105°.
故选B.
∴∠CDB=∠CBD=45°,
∵AC⊥BD于点O,
∴∠COD=90°,∠OCD=45°,△COD是等腰直角三角形,
∴CD=
| 2 |
∵AD=
| 2 |
∴AD=
| 2 |
| 2 |
| 2 |
在直角△AOD中,∠AOD=90°,
∴sin∠OAD=
| OD |
| AD |
| 1 |
| 2 |
∴∠OAD=30°,
∴∠ODA=90°-30°=60°,
∴∠ADC=∠ODA+∠CDO=60°+45°=105°.
故选B.
点评:本题考查了等腰直角三角形的判定与性质,锐角三角函数的定义,难度适中.得出AD=2OD是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
化简(
)2的结果为( )
| 22 |
| A、2 | B、4 | C、8 | D、16 |
cosA=
(A为锐角),则∠A的度数为( )
| ||
| 2 |
| A、60° | B、30° |
| C、45° | D、30°或60° |
在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C为第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是( )
| A、m≥0 | ||||
B、m≥
| ||||
C、m≤
| ||||
D、0≤m≤
|
下列真命题中逆命题也是真命题的是( )
| A、对顶角相等 |
| B、全等三角形对应角相等 |
| C、全等三角形对应边相等 |
| D、等边三角形是锐角三角形 |
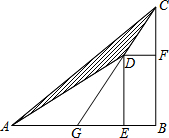 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?( )
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?( )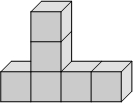 如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
如图是由一些棱长都为1cm的小正方体组合成的简单几何体.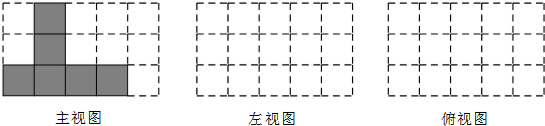
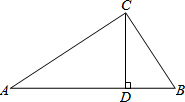 在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15,
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15,