题目内容
 在矩形ABCD中,BC=8cm,对角线AC比AB多4cm,BE⊥AC于点E,求BE的长.
在矩形ABCD中,BC=8cm,对角线AC比AB多4cm,BE⊥AC于点E,求BE的长.考点:矩形的性质,勾股定理
专题:
分析:设AB=x,表示出AC=x+4,然后在Rt△ABC中利用勾股定理列出方程求出x,再根据△ABC的面积列出方程求解即可.
解答:解:设AB=x,则AC=x+4,
在Rt△ABC中,AB2+BC2=AC2,
即x2+82=(x+4)2,
解得x=6,
∴AB=6,AC=6+4=10,
∵BE⊥AC,
∴S△ABC=
AC•BE=
AB•BC,
∴
×10•BE=
×6•8,
解得BE=4.8.
在Rt△ABC中,AB2+BC2=AC2,
即x2+82=(x+4)2,
解得x=6,
∴AB=6,AC=6+4=10,
∵BE⊥AC,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得BE=4.8.
点评:本题考查了矩形的性质,勾股定理,利用勾股定理列出方程是解题的关键,难点在于利用三角形的面积列出方程.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.
如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.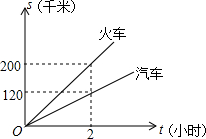 已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图.
已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图. 如图,△ABC中,D、E分别是AB、AC的中点,若△ADE的面积为2,则四边形DECB的面积是
如图,△ABC中,D、E分别是AB、AC的中点,若△ADE的面积为2,则四边形DECB的面积是