Question

1．如图1，在直角坐标系中，直线y=ax+b与x轴负半轴、y轴正半轴分别交于点B、A，以B为直角顶点在直线AB的左侧作等腰直角△ABC．
（1）若a=b=2，求点C的坐标；
（2）如图2，若AC交x轴于M，点D是线段CM上一点，以BD为边在第二象限作正方形BDEF，连接BE、DF交于点Q，连AQ．试求$\frac{AQ}{BD}$的值；
（3）在（1）的条件下，y=kx+3k与直线AB交于点P，那么是否存在这样的点P．使两条直线相交所成的锐角不小于45°？若存在，求出点P的横坐标满足的条件；若不存在，请说明理由．

Answer 1

分析 （1）过点C作CD⊥OB，垂足为D．由a、b的值得到一次函数的解析式，然后可求得点AB的坐标，接下来证明△ABC为等腰直角三角形，△DCB≌△OBA，依据全等三角形的性质可知DC=OB=1，BD=OA=2，故此可得到点C的坐标；
（2）连结AF、QA．首先证明△DCB≌△FAB，从而得到∠BDC=∠BFA，于是可判定点D、B、A、F四点共圆，则QD=QF=QB=QA，然后依据正方形的性质可求得BD：QB，最后通过等量代换可得到问题的答案；
（3）如图3所示：当∠DPF=45时，过点D作DF⊥AB，垂足为F，过点P作PE⊥OB，垂足为E．由直线的解析式可知直线l必过点D（-3，0），接下来，证明△DFB∽△AOB，由相似三角形的性质可求得BF、DF的长，从而得到BP的长，接下来证明△PEB∽△AOB可求得BE的长，从而得到点P的横坐标；如图4所示：当∠DPB=45°时，取OF=OB，过点F作FE⊥AB，垂足为E．依据三角形的外角的性质可知∠PDB=∠PBF，然后在△AOB中依据面积法可求得EF的长，然后由BF的长可求得BE的长，从而可得到tan∠EBF=$\frac{1}{3}$，于是得到k=$\frac{1}{3}$，最后将y=$\frac{1}{3}$x+1与y=2x+2联立可求得点P的横坐标，然后根据两次求得的P的坐标，可确定出点P的横坐标的取值范围．

解答 解：（1）如图1所示：过点C作CD⊥OB，垂足为D．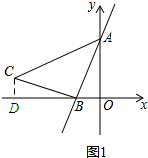

∵a=b=2，
∴直线AB的解析式为y=2x+2．
∵当x=0时，y=2，
∴A（0，2）．
∴OA=2．
当y=0时，2x+2=0，解得x=-1，
∴B（-1，0）．
∴OB=1．
∵△ABC为等腰直角三角形，
∴BC=AB，∠CBD+∠AB0=90°．
又∵∠DCB+∠CBD=90°，
∴∠DCB=∠ABO．
在△DCB和△OBA中$\left\{\begin{array}{l}{∠CDB=∠BOA}\\{∠DCB=∠OBA}\\{BC=AB}\end{array}\right.$，
∴△DCB≌△OBA．
∴DC=OB=1，BD=OA=2．
∴OD=3．
∴点C的坐标为（-3，1）．
（2）如图2所示，连结AF、QA．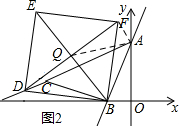

∵∠DBF=∠CBA=90°，
∴∠DBF-∠CBF=∠CBA-∠CBF，即∠DBC=∠FBA．
在△DCB和△FAB中$\left\{\begin{array}{l}{BC=AB}\\{∠DBC=∠FBA}\\{BD=BF}\end{array}\right.$，
∴△DCB≌△FAB．
∴∠BDC=∠BFA．
∴点D、B、A、F四点共圆．
∴QD=QF=QB=QA．
∵$\frac{QB}{BD}=\frac{\sqrt{2}}{2}$，
∴$\frac{QA}{BD}=\frac{\sqrt{2}}{2}$．
（3）如图3所示：当∠DPF=45时，过点D作DF⊥AB，垂足为F，过点P作PE⊥OB，垂足为E．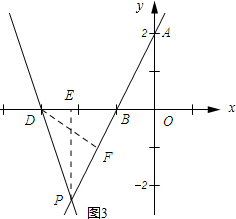

∵y=kx+3k=k（x+3）
∴当x=-3时，y=0．
∴直线y=kx+3k必过点D（-3，0）．
∴BD=2．
在Rt△AOB中，AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{5}$．
∵∠DBF=∠ABO，∠DFB=∠AOB，
∴△DFB∽△AOB．
∴$\frac{DB}{AB}=\frac{FB}{OB}$=$\frac{DF}{AO}$即$\frac{2}{\sqrt{5}}=\frac{BF}{1}$=$\frac{DF}{2}$，解得：BF=$\frac{2\sqrt{5}}{5}$，DF=$\frac{4\sqrt{5}}{5}$．
∵∠DPF=45°，∠DFP=90°，
∴DF=FP．
∴BP=$\frac{6\sqrt{5}}{5}$．
∵∠PBE=∠ABO，∠PEB=∠AOB，
∴△PEB∽△AOB．
∴$\frac{BP}{AB}=\frac{BE}{OB}$，即$\frac{\frac{6\sqrt{5}}{5}}{\sqrt{5}}=\frac{EB}{1}$，解得：BE=$\frac{6}{5}$．
∴点E的坐标为（-$\frac{11}{5}$，0）．
如图4所示：当∠DPB=45°时，取OF=OB，过点F作FE⊥AB，垂足为E．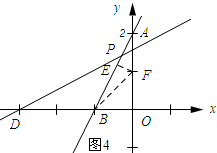

∵OB=OF，∠BOF=90°，
∴∠FBO=45°．
∵∠D+∠DPB=∠PBF+∠FBO，∠DPB=∠FBO=45°，
∴∠PDB=∠PBF．
∵S_△AOB=$\frac{1}{2}$OB•OA=$\frac{1}{2}$OB•OF+$\frac{1}{2}$AB•EF，
∴$\frac{1}{2}$×$\sqrt{5}$×EF=$\frac{1}{2}$，解得：EF=$\frac{\sqrt{5}}{5}$．
∵BF=$\sqrt{O{B}^{2}+O{F}^{2}}$=$\sqrt{2}$，
∴BE=$\sqrt{B{F}^{2}-E{F}^{2}}$=$\frac{3\sqrt{5}}{5}$．
∴tan∠EBF=$\frac{EF}{EB}$=$\frac{1}{3}$．
∴tan∠PDB=$\frac{1}{3}$．
∴直线l的解析式为y=$\frac{1}{3}$x+1．
将y=$\frac{1}{3}$x+1与y=2x+2联立，解得：x=-$\frac{3}{5}$．
所以当-$\frac{11}{5}$≤p的横坐标≤-$\frac{3}{5}$时，使两条直线相交所成的锐角不小于45°．

点评 本题主要考查的是一次函数的综合应用，解答本题主要应用了相似三角形的性质和判断、勾股定理、锐角三角函数的定义，四点共圆的条件，得到△DCB≌△OBA是解答问题（1）的关键，证得点D、B、A、F四点共圆是解题答问题（2）的关键，找出图3和图4中的相似三角形，求得相关线段的长是解答问题的（3）的关键．