题目内容
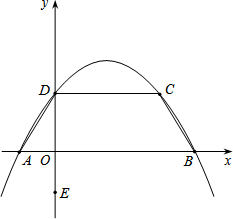 如图,抛物线y=-
如图,抛物线y=-| 5 |
| 24 |
| 5 |
| 4 |
| 10 |
| 3 |
| 7 |
| 3 |
(1)直接写出A、B、D三点的坐标;
(2)直接写出直线l的解析式;
(3)若点P在直线l上,且在x轴上方,tan∠OPB=
| 4 |
| 3 |
考点:二次函数综合题
专题:
分析:(1)利用二次函数与坐标轴交点求法分别得出即可;
(2)利用等腰梯形的性质以及二次函数对称性得出G点坐标,进而求出即可;
(3)首先得出△OPB∽△PHB,进而得出关于a,b的等式求出即可.
(2)利用等腰梯形的性质以及二次函数对称性得出G点坐标,进而求出即可;
(3)首先得出△OPB∽△PHB,进而得出关于a,b的等式求出即可.
解答: 解:(1)由题意可知:D点在y轴上,当x=0时,y=
解:(1)由题意可知:D点在y轴上,当x=0时,y=
,
所以D的坐标为(0,
)
令y=0,有0=-
x2+
x+
,
化简可得:x2-6x-16=(x+2)(x-8)=0,
解得:x1=-2,x2=8,
故A和B的坐标分别为:(-2,0)和(8,0);
(2)如图1,∵y=-
x2+
x+
,对称轴为:x=-
=3,
∴C点的横坐标为:6,则C(6,
),
设x=3与梯形下底和上底分别交于E和F点,E点坐标为(3,0),F点的坐标为(3,
).
而过l点的直线要平分梯形,该直线必须过EF的中点G,使得该直线与梯形以及x=3形成的两个三角形全等.
显然G的坐标为(3,
).
设直线解析式为y=kx+b,
将(0,-
)和(3,
)代入得出:
,
解得:
,
故直线l的解析式为:y=
x-
;

(3)如图2,设直线l交x轴于H点,
∵直线l的解析式为:y=
x-
,
∴tan∠PHB=
,H(
,0),
∴BH=8-
=
,
∵tan∠OPB=
,tan∠PHB=
,
∴∠OPB=∠PHB,
∵∠PBA=∠HBP,
∴△OPB∽△PHB,
∴
=
,
∴PB2=OB×HB=50,
设P的坐标为(a,b),
则(a-8)2+b2=50,
又∵(a,b)在直线l上,
所以满足b=
-
,
则(a-8)2+(
-
)2=50,
解得:a1=1,a2=7,
而a=1时b=-1在x轴下方,
所以a只能取7,此时b=7,
所以P点的坐标为(7,7).
 解:(1)由题意可知:D点在y轴上,当x=0时,y=
解:(1)由题意可知:D点在y轴上,当x=0时,y=| 10 |
| 3 |
所以D的坐标为(0,
| 10 |
| 3 |
令y=0,有0=-
| 5 |
| 24 |
| 5 |
| 4 |
| 10 |
| 3 |
化简可得:x2-6x-16=(x+2)(x-8)=0,
解得:x1=-2,x2=8,
故A和B的坐标分别为:(-2,0)和(8,0);
(2)如图1,∵y=-
| 5 |
| 24 |
| 5 |
| 4 |
| 10 |
| 3 |
| b |
| 2a |
∴C点的横坐标为:6,则C(6,
| 10 |
| 3 |
设x=3与梯形下底和上底分别交于E和F点,E点坐标为(3,0),F点的坐标为(3,
| 10 |
| 3 |
而过l点的直线要平分梯形,该直线必须过EF的中点G,使得该直线与梯形以及x=3形成的两个三角形全等.
显然G的坐标为(3,
| 5 |
| 3 |
设直线解析式为y=kx+b,
将(0,-
| 7 |
| 3 |
| 5 |
| 3 |
|
解得:
|
故直线l的解析式为:y=
| 4 |
| 3 |
| 7 |
| 3 |

(3)如图2,设直线l交x轴于H点,
∵直线l的解析式为:y=
| 4 |
| 3 |
| 7 |
| 3 |
∴tan∠PHB=
| 4 |
| 3 |
| 7 |
| 4 |
∴BH=8-
| 7 |
| 4 |
| 25 |
| 4 |
∵tan∠OPB=
| 4 |
| 3 |
| 4 |
| 3 |
∴∠OPB=∠PHB,
∵∠PBA=∠HBP,
∴△OPB∽△PHB,
∴
| PB |
| OB |
| HB |
| PB |
∴PB2=OB×HB=50,
设P的坐标为(a,b),
则(a-8)2+b2=50,
又∵(a,b)在直线l上,
所以满足b=
| 4a |
| 3 |
| 7 |
| 3 |
则(a-8)2+(
| 4a |
| 3 |
| 7 |
| 3 |
解得:a1=1,a2=7,
而a=1时b=-1在x轴下方,
所以a只能取7,此时b=7,
所以P点的坐标为(7,7).
点评:此题主要考查了二次函数综合以及相似三角形的判定以及待定系数法求一次函数解析式等知识,得出△OPB∽△PHB是解题关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
满足不等式6x-3>4x-4的解集是( )
A、x>
| ||
B、x>-
| ||
C、x<-
| ||
D、x<
|
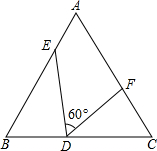 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.
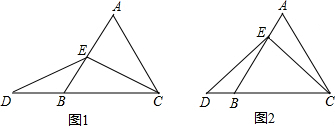
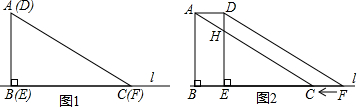
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.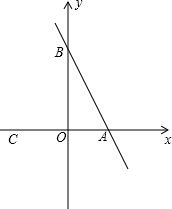 已知在平面直角坐标系中,点A、B的坐标分别为A(3,0)、B(O,4),点C的坐标为C(-2,O),点P是直线AB上的一动点,直线CP与y轴交于点D.
已知在平面直角坐标系中,点A、B的坐标分别为A(3,0)、B(O,4),点C的坐标为C(-2,O),点P是直线AB上的一动点,直线CP与y轴交于点D.