题目内容
17.计算:(1)$\frac{1}{2}$$\sqrt{10}$×(3$\sqrt{15}$-5$\sqrt{\frac{3}{5}}$);
(2)$\sqrt{18}$-$\sqrt{\frac{9}{2}}$-$\frac{\sqrt{3}+\sqrt{6}}{\sqrt{3}}$+$\sqrt{(\sqrt{2}-1)^{2}}$.
分析 (1)先化简二次根式,在合并括号内二次根式,最后计算乘法即可;
(2)先化简各二次根式,再去括号计算二次根式的加减法.
解答 解:(1)原式=$\frac{\sqrt{10}}{2}$×(3$\sqrt{15}$-$\sqrt{15}$)
=$\frac{\sqrt{10}}{2}$×2$\sqrt{15}$
=5$\sqrt{6}$;
(2)原式=3$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$-(1+$\sqrt{2}$)+$\sqrt{2}$-1
=$\frac{3\sqrt{2}}{2}$-1-$\sqrt{2}$+$\sqrt{2}$-1
=$\frac{3\sqrt{2}}{2}$-2.
点评 本题主要考查二次根式的混合运算,二次根式的混合运算应注意以下几点:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式“,多个不同类的二次根式的和可以看作“多项式“.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
12.在Rt△ABC中,∠C=90°,a=5,c=13,则b的长为( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
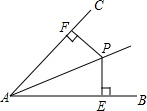 如图,点P是∠BAC的角平分线上的一点,若PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE=PF.理由是角平分线上的点到角的两边的距离相等.
如图,点P是∠BAC的角平分线上的一点,若PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE=PF.理由是角平分线上的点到角的两边的距离相等.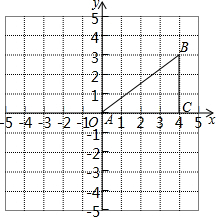 如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.
如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.