题目内容
我县化工园区一化工厂,组织20辆汽车装运A、B、C三种化学物资共200吨到某地.按计划20辆汽车都要装运,每辆汽车只能装运同一种物资且必须装满.请结合表中提供的信息,解答下列问题:
(1)设装运A种物资的车辆数为x,装运B种物资的车辆数为y.求y与x的函数关系式;
(2)如果装运A种物资的车辆数不少于5辆,装运B种物资的车辆数不少于4辆,若要求总运费最少,应如何安排使得总运费最少,并求出最少总运费.
(1)设装运A种物资的车辆数为x,装运B种物资的车辆数为y.求y与x的函数关系式;
(2)如果装运A种物资的车辆数不少于5辆,装运B种物资的车辆数不少于4辆,若要求总运费最少,应如何安排使得总运费最少,并求出最少总运费.
| 物资种类 | A | B | C |
| 每辆汽车运载量(吨) | 12 | 10 | 8 |
| 每吨所需运费(元/吨) | 240 | 320 | 200 |
考点:一次函数的应用
专题:
分析:(1)表示装运C的车辆数为(20-x-y),然后根据物资总量为200吨列出方程,整理即可得解;
(2)先求出x的取值范围,再列式总量得到总运费表达式,然后根据一次函数增减性求出安排方案和最少运费.
(2)先求出x的取值范围,再列式总量得到总运费表达式,然后根据一次函数增减性求出安排方案和最少运费.
解答:解:(1)根据题意得:12x+10y+8(20-x-y)=200,
12x+10y+160-8x-8y=200,
2x+y=20,
所以,y=20-2x;
(2)由题意得
,
解得5≤x≤8;
设总运费为M,
则M=12×240x+10×20(20-2x)+8×200(20-x+2x-20),
即M=-1920x+64000,
∵M是x一次函数,且M随x的增大而减小,x取正整数,
∴当x=8时,M最小,最小值为48640元,
即装运A种物资的车8辆,装运B种物资的车4辆,装运C种物资的车8辆.
12x+10y+160-8x-8y=200,
2x+y=20,
所以,y=20-2x;
(2)由题意得
|
解得5≤x≤8;
设总运费为M,
则M=12×240x+10×20(20-2x)+8×200(20-x+2x-20),
即M=-1920x+64000,
∵M是x一次函数,且M随x的增大而减小,x取正整数,
∴当x=8时,M最小,最小值为48640元,
即装运A种物资的车8辆,装运B种物资的车4辆,装运C种物资的车8辆.
点评:本题考查了一次函数的应用,利用一次函数的增减性求最值问题,难点在于表示出装运C物资的车辆数和(2)求出x的取值范围.

练习册系列答案
相关题目
下列说法正确的是( )
| A、ab+c是二次三项式 | ||
| B、多项式2x2+3y2的次数是4 | ||
| C、5是单项式 | ||
D、
|
 如图,一艘货船以36海里/时的速度在海面上航行,当他行驶到A处时,发现它的东北方向有一灯塔B,获准继续向北航行四十分钟后,到达C处发现灯塔B在它北边东75度方向.求此时货轮与灯塔B的距离(结果精确到0.1海里).
如图,一艘货船以36海里/时的速度在海面上航行,当他行驶到A处时,发现它的东北方向有一灯塔B,获准继续向北航行四十分钟后,到达C处发现灯塔B在它北边东75度方向.求此时货轮与灯塔B的距离(结果精确到0.1海里).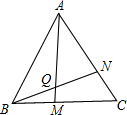 如图,△ABC为等边三角形,点M,N分别在BC,AC上,且BM=CN,AM与BN交于Q点.则∠AQN的度数为
如图,△ABC为等边三角形,点M,N分别在BC,AC上,且BM=CN,AM与BN交于Q点.则∠AQN的度数为 已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=30°.在图中作弦AD,使AD=1,并求∠CAD的度数.
已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=30°.在图中作弦AD,使AD=1,并求∠CAD的度数.