题目内容
4. 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:(1)A、B两城之间距离是多少千米?
(2)求乙车出发多长时间追上甲车?
(3)直接写出甲车出发多长时间,两车相距20千米.
分析 (1)根据图象即可得出结论.
(2)先求出甲乙两人的速度,再列出方程即可解决问题.
(3)根据y甲-y乙=20或y乙-y甲=20,列出方程即可解决.
解答 解: (1)由图象可知A、B两城之间距离是300千米.
(1)由图象可知A、B两城之间距离是300千米.
(2)设乙车出发x小时追上甲车.
由图象可知,甲的速度=$\frac{300}{5}$=60千米/小时.
乙的速度=$\frac{300}{3}$=100千米/小时.
由题意60(x+1)=100x
解得x=1.5小时.
(3)设y甲=kx+b,则$\left\{\begin{array}{l}{5k+b=0}\\{10k+b=300}\end{array}\right.$解得$\left\{\begin{array}{l}{k=60}\\{b=-300}\end{array}\right.$,
∴y甲=60x-300,
设y乙=k′x+b′,则$\left\{\begin{array}{l}{6k′+b′=0}\\{9k′+b′=300}\end{array}\right.$,解得$\left\{\begin{array}{l}{k′=100}\\{b′=-600}\end{array}\right.$,
∴y乙=100x-600,
∵两车相距20千米,
∴y甲-y乙=20或y乙-y甲=20或y甲=20或y甲=280,
即60x-300-(100x-600)=20或100x-600-(60x-300)=20或60x-300=20或60x-300=280
解得x=7或8或$\frac{16}{3}$或$\frac{29}{3}$,
∵7-5=2,8-5=3,$\frac{16}{3}$-5=$\frac{1}{3}$,$\frac{29}{3}$-5=$\frac{14}{3}$
∴甲车出发2小时或3小时或$\frac{1}{3}$小时或$\frac{14}{3}$小时,两车相距20千米.
点评 本题考查一次函数的应用、行程问题等知识,解题的关键是学会利用函数解决实际问题,学会转化的思想,把问题转化为方程,属于中考常考题型.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案| A. | x1=4,x2=-4 | B. | x1=2,x2=-2 | C. | x1=x2=0 | D. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | x+y=3 | B. | x-y=1 | C. | 2x+y=3 | D. | 2x-y=1 |
| A. | 正三角形 | B. | 正方形 | C. | 正六边形 | D. | 正十边形 |
 将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案,设菱形中较小的角为α度,平行四边形中较大的角为β度,那么β可以用含α的代数式表示为β=$\frac{180+α}{2}$.
将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案,设菱形中较小的角为α度,平行四边形中较大的角为β度,那么β可以用含α的代数式表示为β=$\frac{180+α}{2}$.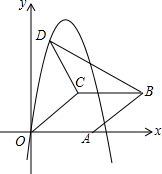 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.