题目内容
14.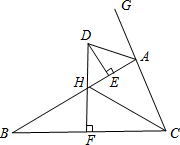 如图,△ABC中,AB>AC,延长CA至点G,边BC的垂直平分线DF与∠BAG的角平分线交于点D,与AB交于点H,F为垂足,DE⊥AB于E.下列说法正确的是③.(填序号)
如图,△ABC中,AB>AC,延长CA至点G,边BC的垂直平分线DF与∠BAG的角平分线交于点D,与AB交于点H,F为垂足,DE⊥AB于E.下列说法正确的是③.(填序号)①BH=FC;②∠GAD=$\frac{1}{2}$(∠B+∠HCB);③BE-AC=AE;④∠B=∠ADE.
分析 根据线段垂直平分线的性质得到BH=CH,BF=CF,由于CH>CF,于是得到BH>CF,故①错误;根据角平分线的性质和三角形的外角的性质得到∠GAD=$\frac{1}{2}∠$GAB=$\frac{1}{2}$(∠ABC+∠ACB),由于∠ACB>∠HCB,于是得到∠GAD$>\frac{1}{2}$(∠B+∠HCB),故②错误;过D作DN⊥AC,垂足为N,连接DB、DC,推出DN=DF,DB=DC,根据HL证Rt△DBF≌R△DCN,推出BF=CN,根据HL证Rt△DFA≌Rt△DNA,推出AN=AF,于是得到BE=AC+AN=AC+AE,即BE-AC=AE,故③正确;根据余角的性质得到∠ABC=∠HDE,故④错误.
解答 证明:∵DF垂直平分BC,
∴BH=CH,BF=CF,
∵CH>CF,
∴BH>CF,故①错误;
∵∠GAB=∠ABC+∠ACB,AD平分∠GAB,
∴∠GAD=$\frac{1}{2}∠$GAB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠ACB>∠HCB,
∴∠GAD$>\frac{1}{2}$(∠B+∠HCB),故②错误;
过D作DN⊥AC,垂足为N,连接DB、DC,
则DN=DE,DB=DC,
又∵DF⊥AB,DN⊥AC,
∴∠DEB=∠DNC=90°,
在Rt△DBE和Rt△DCN中,
$\left\{\begin{array}{l}{DB=DC}\\{DE=DN}\end{array}\right.$,
∴Rt△DBE≌Rt△DCN(HL),
∴BE=CN,
在Rt△DEA和Rt△DNA中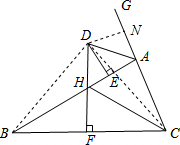 ,
,
$\left\{\begin{array}{l}{AD=AD}\\{DE=DN}\end{array}\right.$,
∴Rt△DEA≌Rt△DNA(HL),
∴AN=AE,
∴BE=AC+AN=AC+AE,
即BE-AC=AE,故③正确;
∵DE⊥AB,
∴∠HDE+∠DHE=∠HBF+∠BHF=90°,
∵∠ABC=∠HDE,故④错误.
故答案为:③.
点评 本题考查了全等三角形的性质和判定,线段的垂直平分线定理,角平分线性质等知识点,会添加适当的辅助线,会利用中垂线的性质找出全等的条件是解此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案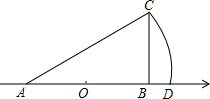 如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )
如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )| A. | $\frac{2\sqrt{3}}{3}-1$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}-1$ |
| A. | 所有的有理数都能用数轴上的点表示 | |
| B. | 符号不同的两个数互为相反数 | |
| C. | 有理数分为正数和负数 | |
| D. | 两数相加,和一定大于任何一个数 |
| A. | 9.6×10 | B. | 96×104 | C. | 9.6×105 | D. | 9.6×106 |
 如图,在△AOC和△BOC中,若∠AOC=∠BOC,添加一个条件AO=BO,使得△AOC≌△BOC.
如图,在△AOC和△BOC中,若∠AOC=∠BOC,添加一个条件AO=BO,使得△AOC≌△BOC.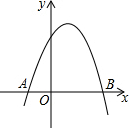 抛物线y=ax2+bx+c(a≠0)与x轴的两个交点分别为A(-1,0)和B(2,0),则一元二次方程ax2+bx+c=0的解为x1=-1,x2=2.
抛物线y=ax2+bx+c(a≠0)与x轴的两个交点分别为A(-1,0)和B(2,0),则一元二次方程ax2+bx+c=0的解为x1=-1,x2=2.
 如图,已知AB=AC,AD是BC边上的中线,求证:AD是∠BAC的角平分线.
如图,已知AB=AC,AD是BC边上的中线,求证:AD是∠BAC的角平分线.