抛物线y=ax2+bx+c与x轴的两个交点分别为A.则一元二次方程ax2+bx+c=0的解为x1=-1.x2=2．题目和参考答案——青夏教育精英家教网—

题目内容

2．

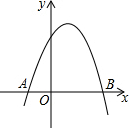抛物线y=ax²+bx+c（a≠0）与x轴的两个交点分别为A（-1，0）和B（2，0），则一元二次方程ax²+bx+c=0的解为x₁=-1，x₂=2．

分析直接利用抛物线与x轴的交点问题求解．

解答解：∵抛物线y=ax²+bx+c（a≠0）与x轴的两个交点分别为A（-1，0）和B（2，0），
∴一元二次方程ax²+bx+c=0的解为x₁=-1，x₂=2．
故答案为x₁=-1，x₂=2．

点评本题考查了抛物线与x轴的交点：从二次函数的交点式y=a（x-x₁）（x-x₂）（a，b，c是常数，a≠0）中能直接得到抛物线与x轴的交点坐标（x₁，0），（x₂，0）．

练习册系列答案

相关题目

12．a为有理数，下列说法中正确的是（　　）

13．

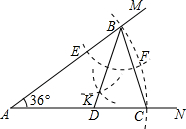如图，小明作图如下：
（1）用量角器作∠MAN=36°；
（2）以A为圆心适当长为半径作圆弧，分别交AM，AN于B，C两点，连结BC；
（3）以B为圆心适当长为半径作圆弧，分别交AB，BC于E，F两点，再分别以E，F为圆心大于$\frac{1}{2}$EF长为半径作圆弧，两条圆弧交于点K，连结BK并延长交AC于点D．
若AD=a，则由以上作图可得AB为（　　）

A．

$\frac{\sqrt{5}-1}{2}$a

B．

$\frac{3-\sqrt{5}}{2}$a

C．

$\frac{\sqrt{5}+1}{2}a$

D．

$\frac{3+\sqrt{5}}{2}$a

10．我区某校为调查学生的视力变化情况，从全校九年级学生中抽取了部分学生，统计了每个人连续三年视力检查的结果，并将所得数据处理后，绘制成折线统计图和扇形统计图如下：

解答下列问题：
（1）该校共抽取了多少名九年级学生？
（2）若该校共有1100名九年级学生，请你估计该校九年级视力不良（4.9以下）的学生大约有多少人？
（3）根据统计图提供的信息，谈谈你的感想（不超过30字）．

17．

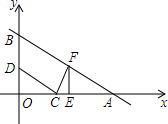如图，在平面直角坐标系中，一次函数图象与x轴，y轴分别交于点A（8，0），B（0，4），点C的坐标为（3，0），动点D是射线BO上一个动点，连结CD，过点C作CD⊥FC，交一次函数图象于点F．
（1）求这个一次函数的解析式；
（2）过点F作FE⊥x轴，垂足为点E，当△OCD与△EFC全等时，求出满足条件的点F的坐标；
（3）点D在运动过程中，是否存在使△ACF是等腰三角形？若存在请求出点F的坐标；不存在，请说明理由．

7．已知点A（-2，y₁），B（-1，y₂）在函数y=$\frac{3}{x}$的图象上，则y₁与y₂的大小关系是（　　）

y₁＞y₂

y₁＜y₂

y₁=y₂

14．

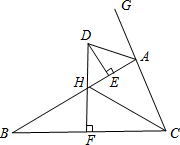如图，△ABC中，AB＞AC，延长CA至点G，边BC的垂直平分线DF与∠BAG的角平分线交于点D，与AB交于点H，F为垂足，DE⊥AB于E．下列说法正确的是③．（填序号）
①BH=FC；②∠GAD=$\frac{1}{2}$（∠B+∠HCB）；③BE-AC=AE；④∠B=∠ADE．

11．不等式3x-1＜5的解集为x＜2．

4．

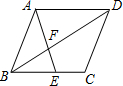如图，平行四边形ABCD中，E是边BC上的点，AE交BD于点F，如果$\frac{BE}{BC}=\frac{2}{3}$，那么$\frac{BF}{FD}$=$\frac{2}{3}$．

试题分类