题目内容
5.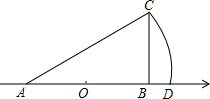 如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )
如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )| A. | $\frac{2\sqrt{3}}{3}-1$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}-1$ |
分析 首先求得AB的长,然后在直角△ABC中利用三角函数即可求得AC的长,则AD=AC即可求得,然后求得OD即可.
解答 解:∵点A表示-1,O是AB的中点,
∴OA=OB=1,
∴AB=2,
在直角△ABC中,AC=$\frac{AB}{cos∠BAC}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}}{3}$,
∴AD=AC=$\frac{4\sqrt{3}}{3}$,
∴OD=$\frac{4\sqrt{3}}{3}-1$.
故选D.
点评 本题考查了三角函数,在直角三角形中利用三角函数求得AC的长是关键.

练习册系列答案
相关题目
15.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-7)=0的两根,则这个三角形的周长是( )
| A. | 12 | B. | 12或17 | C. | 17 | D. | 19 |
16. 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )| A. | 28m | B. | 29m | C. | 30m | D. | 31m |
13.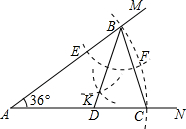 如图,小明作图如下:
如图,小明作图如下:
(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
 如图,小明作图如下:
如图,小明作图如下:(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{3-\sqrt{5}}{2}$a | C. | $\frac{\sqrt{5}+1}{2}a$ | D. | $\frac{3+\sqrt{5}}{2}$a |
15.已知(-3,y1),(-15,y2),(2,y3)在反比例函数y=-$\frac{a^2}{x}$上,则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
 某商场为促进消费,方便消费者停车,拟将商场门口某区域改建为停车场.如图,已知该区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入,为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡的倾斜角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考数据tan5.711°≈0.1000,sin5.711°≈0.09951,cos5.711°≈0.9950).
某商场为促进消费,方便消费者停车,拟将商场门口某区域改建为停车场.如图,已知该区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入,为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡的倾斜角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考数据tan5.711°≈0.1000,sin5.711°≈0.09951,cos5.711°≈0.9950).
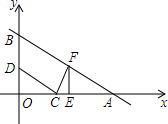 如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.
如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.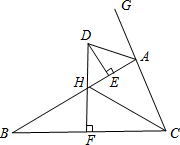 如图,△ABC中,AB>AC,延长CA至点G,边BC的垂直平分线DF与∠BAG的角平分线交于点D,与AB交于点H,F为垂足,DE⊥AB于E.下列说法正确的是③.(填序号)
如图,△ABC中,AB>AC,延长CA至点G,边BC的垂直平分线DF与∠BAG的角平分线交于点D,与AB交于点H,F为垂足,DE⊥AB于E.下列说法正确的是③.(填序号)