题目内容
19.已知5|x+y-3|+$\frac{1}{2}$(x-2y)2=0,则x,y的值分别为2;1.分析 利用非负数的性质列出方程组,求出方程组的解即可得到x与y的值.
解答 解:∵5|x+y-3|+$\frac{1}{2}$(x-2y)2=0,
∴$\left\{\begin{array}{l}{x+y=3①}\\{x=2y②}\end{array}\right.$,
把②代入①得:2y+y=3,即y=1,
把y=1代入②得:x=2,
故答案为:2;1.
点评 此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
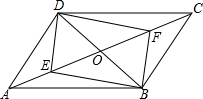 如图,?ABCD中,对角线AC、BD相交于点O,若BD=12cm,AC=20cm
如图,?ABCD中,对角线AC、BD相交于点O,若BD=12cm,AC=20cm 如图,AD⊥BC于D,BE⊥AC于E,AD、BE交于F,AD=BD.试判断:BF与AC的数量关系,并加以证明.
如图,AD⊥BC于D,BE⊥AC于E,AD、BE交于F,AD=BD.试判断:BF与AC的数量关系,并加以证明.