Question

15．如图（1）是一种广场三联漫步机，其侧面示意图如图（2）所示，其中AB=AC=120cm，BC=80cm，AD=30cm，∠DAC=90°．求点D到地面的高度是多少？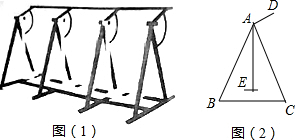

Answer 1

分析 首先过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．进而得出AF的长，再利用相似三角形的判定与性质得出AH的长即可得出答案．

解答 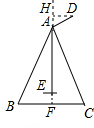解：过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．
∵AF⊥BC，垂足为F，
∴BF=FC=$\frac{1}{2}$BC=40cm．
根据勾股定理，得AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{12{0}^{2}-4{0}^{2}}$=80$\sqrt{2}$（cm），
∵∠DHA=∠DAC=∠AFC=90°，
∴∠DAH+∠FAC=90°，∠C+∠FAC=90°，
∴∠DAH=∠C，
∴△DAH∽△ACF，
∴$\frac{AH}{FC}$=$\frac{AD}{AC}$，
∴$\frac{AH}{40}$=$\frac{30}{120}$，
∴AH=10cm，
∴HF=（10+80$\sqrt{2}$）cm．
答：D到地面的高度为（10+80$\sqrt{2}$）cm．

点评 此题主要考查了相似三角形的应用以及勾股定理，根据题意得出△DAH∽△ACF是解题关键．