题目内容
5.填空(1)$\frac{ab}{{a}^{2}}=\frac{b}{()}$;
(2)$\frac{{x}^{3}}{{x}^{2}+xy}=\frac{()}{x+y}$;
(3)$\frac{x+y}{xy}=\frac{{x}^{2}+xy}{()}$;
(4)$\frac{x+y}{x-y}=\frac{()}{{x}^{2}-2xy+{y}^{2}}$.
分析 (1)分子、分母同时乘以a;
(2)分子、分母同时除以x;
(3)分子、分母同时乘以x;
(4)分子、分母同时乘以(x-y).
解答 解:(1)$\frac{ab}{{a}^{2}}$=$\frac{b}{a}$;
故答案是:a;
(2)$\frac{{x}^{3}}{{x}^{2}+xy}$=$\frac{{x}^{2}}{x+y}$;
故答案是:x2;
(3)$\frac{x+y}{xy}$=$\frac{{x}^{2}+xy}{{x}^{2}y}$;
故答案是:x2y;
(4)$\frac{x+y}{x-y}$=$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$.
故答案是:x2-y2.
点评 本题考查了分式的基本性质.注意:无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项.

练习册系列答案
相关题目
13.如何平移抛物线y=-2x2-1得到抛物线y=-2x2+4x-1呢?( )
| A. | 向右平移4个单位 | |
| B. | 先向左平移1个单位,再向上平移2个单位 | |
| C. | 向左平移4个单位 | |
| D. | 先向右平移1个单位,再向上平移2个单位 |
20.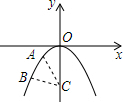 如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )
如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )
 如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )
如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 5 |
 如图,已知AB,CD,EF相交于点O,AB⊥EF于O,ON平分∠COF,OM平分∠DON.
如图,已知AB,CD,EF相交于点O,AB⊥EF于O,ON平分∠COF,OM平分∠DON.