题目内容
20．
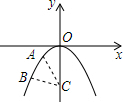如图，已知抛物线y=-x2上有A，B两点，其横坐标分别为-1，-2；在y轴上有一动点C，则AC+BC的最小值为（ ）| A． | 2$\sqrt{2}$ | B． | 3$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 5 |
分析 找出点A关于y轴的对称点A′，连接A′B与y轴相交于点C，根据轴对称确定最短路线问题，点C即为使AC+BC最短的点，再根据抛物线解析式求出点A′、B的坐标，然后利用勾股定理列式计算即可得解．
解答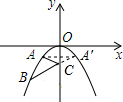 
解：如图，点A关于y轴的对称点A′的横坐标为1，
连接A′B与y轴相交于点C，点C即为使AC+BC最短的点，
当x=-1时，y=-1，
当x=-2时，y=-4，
所以，点A′（1，-1），B（-2，-4），
由勾股定理得，A′B=$\sqrt{（1+2）^{2}+（-1+4）^{2}}$=3$\sqrt{2}$．
故选B．
点评 本题考查了轴对称确定最短路线问题，二次函数的性质，熟记确定出最短路径的方法和二次函数的对称性确定出点C的位置是解题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
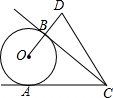如图，CA、CB分别切⊙O于点A、B，延长0B到点D，使BD=OB，∠DCA=60°，求∠D的度数．
画出如图所示几何体的主视图、左视图和俯视图．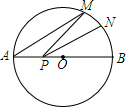
如图，AB是⊙O的直径，AB=10，点M在⊙O上，∠MAB=30°，N是弧MB的中点，P是直径AB上的一动点，若MN=2，则△PMN周长的最小值为5$\sqrt{2}$+2．