题目内容
我们把分子为1的分数叫做单位分数.如
,
,
…,任何一个单位分数都可以拆分成两个不同的单位分数的和,如
=
+
,
=
+
,
=
+
,…
(1)根据对上述式子的观察,你会发现
=
+
.请写出□,○所表示的数;
(2)思考,单位分数
(n是不小于2的正整数)=
+
,请写出△,☆所表示的式.
(3)计算:
+
+
+…+
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
(1)根据对上述式子的观察,你会发现
| 1 |
| 5 |
| 1 |
| □ |
| 1 |
| ○ |
(2)思考,单位分数
| 1 |
| n |
| 1 |
| △ |
| 1 |
| ☆ |
(3)计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 101×102 |
考点:有理数的混合运算
专题:新定义
分析:(1)观察上述式子,确定出□,○所表示的数即可;
(2)归纳总结得到一般性规律,确定出□,○所表示的数即可;
(3)原式拆项变形后,抵消合并即可得到结果.
(2)归纳总结得到一般性规律,确定出□,○所表示的数即可;
(3)原式拆项变形后,抵消合并即可得到结果.
解答:解:(1)根据题意得:
=
+
,
则□,○所表示的数分别为6,30;
(2)根据题意得:
=
-
,
则□,○所表示的数分别为n+1,n(n+1);
(3)原式=1-
+
-
+…+
-
=1-
=
.
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 30 |
则□,○所表示的数分别为6,30;
(2)根据题意得:
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n(n+1) |
则□,○所表示的数分别为n+1,n(n+1);
(3)原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 101 |
| 1 |
| 102 |
| 1 |
| 102 |
| 101 |
| 102 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
若x2+x-1=0,则3x2+3x-6的值等于( )
| A、-3 | B、3 | C、-5 | D、5 |
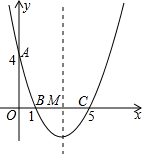 如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.